Concise formula for the Zernike coefficients of scaled pupils

Augustus J.E.M. Janssen; Peter Dirksen

doi:10.1117/1.2345672

1 July 2006 Concise formula for the Zernike coefficients of scaled pupils

Augustus J.E.M. Janssen, Peter Dirksen

Journal of Micro/Nanolithography, MEMS, and MOEMS, Vol. 5, Issue 3, 030501 (July 2006). https://doi.org/10.1117/1.2345672

Abstract

Modern steppers and scanners have a projection lens whose numerical aperture (NA) can be varied so as to optimize the image performance for certain lithographic features. Thus a variable fraction of the aberrations is actually involved in the imaging process. In this letter, we present a concise formula for the NA scaling of the Zernike coefficients. In addition, we apply our results to the Strehl ratio.

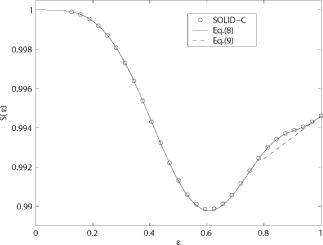
1. Introduction

It is well known that different lithographic features have different optimal settings of the numerical aperture (NA) and illumination condition.^{1, 2} Typically the depth of focus or the process latitudes are optimized. To achieve the optimal settings, modern steppers and scanners have a projection lens with a variable numerical aperture, where the NA value can be reduced to about 70% of its maximum value. As a consequence, a smaller fraction of the lens pupil and a corresponding smaller fraction of the phase aberrations is actually involved in the imaging process.

In the literature (see Ref. 3 for a survey) the problem of computing the aberration Zernike coefficients of scaled pupils has been discussed at various places. The recent result of Dai³ gives the Zernike coefficients of the scaled pupil in terms of those of the unscaled pupil in analytic form [see Eq. 18].

In this letter we give an alternative expression for Dai’s result. Our main result in Eq. 4 agrees mathematically with Dai’s Eq. 18 but has the advantage that it is very simple and direct in terms of Zernike polynomials. Thus it leads to the simple and explicit results in Eqs. 7, 9 from which the sensitivity of the aberration coefficients and Strehl ratios can be assessed when NA is close to its maximum value. The short and elegant proof of our main result in Eq. 4 is given in Appendix A.

2. Zernike Coefficients of Scaled Pupils

We consider a pupil function

Eq. 1

P (ρ, θ) = \exp {i Φ (ρ, θ)},

on a unit disk

0 ⩽ ρ ⩽ 1

with real phase

Φ

, and we assume that

Φ

is expanded as a Zernike series according to:

Eq. 2

Φ (ρ, θ) = \sum_{n, m} α_{n}^{m} R_{n}^{m} (ρ) \cos (m θ),

where

m

and

n

are integers with

n - m

being even and

⩾ 0

, and

R_{n}^{m} (ρ)

denotes the Zernike radial polynomial⁴ of azimuthal order

m

and degree

n

. For simplicity we only consider cosin terms. Scaling to a smaller pupil with relative size

ϵ = NA ∕ {NA}_{\max} ⩽ 1

means that we have to expand the scaled phase

Φ (ϵ ρ, θ)

into a Zernike expansion:

Eq. 3

Φ (ϵ ρ, θ) = \sum_{n, m} α_{n}^{m} (ϵ) R_{n}^{m} (ρ) \cos (m θ), 0 ⩽ ρ ⩽ 1, 0 ⩽ θ ⩽ 2 π .

The problem is how to express the Zernike coefficients

α_{n}^{m} (ϵ)

of the scaled pupil function in terms of the Zernike coefficients

α_{n}^{m}

of the unscaled pupil function. In the Appendix A we prove our main result:

Eq. 4

α_{n}^{m} (ϵ) = \sum_{n^{'}} α_{n^{'}}^{m} [R_{n^{'}}^{n} (ϵ) - R_{n^{'}}^{n + 2} (ϵ)], n = m, m + 2, \dots,

where the summation is over

n^{'} = n, n + 2, \dots

, and where we use the convention that

R_{n}^{n + 2} \equiv 0

. We note that (1) the entries

R_{n^{'}}^{n} (ϵ) - R_{n^{'}}^{n + 2} (ϵ)

do not depend on

m

; we consider them only for

n, n^{'} = m, m + 2, \dots

, and (2)

α_{n}^{m} (ϵ = 1) = α_{n}^{m}

since all involved Zernike polynomials, except

R_{n}^{n + 2} (ϵ) \equiv 0

, equal 1 at

ϵ = 1

.

3. Examples and Sensitivity Analysis

Figure 1 shows an example where we scale low-order coma $α_{3}^{1} (ϵ)$ with $α_{3}^{1} = 2 π (0.016)$ and $α_{5}^{1} = 2 π (0.016)$ . For this special case, Eq. 4 and Dai’s Eq. 18 become

Eq. 5

α_{3}^{1} (ϵ) = α_{3}^{1} R_{3}^{3} (ϵ) + α_{5}^{1} [R_{5}^{3} (ϵ) - R_{5}^{5} (ϵ)]

and

Eq. 6

α_{3}^{1} (ϵ) = ϵ^{3} [α_{3}^{1} + 4 α_{5}^{1} (ϵ^{2} - 1)],

respectively. Both equations give an identical result, as

R_{3}^{3} (ϵ) = ϵ^{3}

and

R_{5}^{3} (ϵ) - R_{5}^{5} (ϵ) = 4 ϵ^{3} (ϵ^{2} - 1)

.

Fig. f1

Scaling low-order coma $α_{3}^{1} (ϵ)$ when $α_{3}^{1} = 2 π (0.016)$ and $α_{5}^{1} = 2 π (0.016)$ . The solid line represents Eq. 4, the dashed line is the tangent line given by Eq. 7, and Eq. 18 is represented by circles.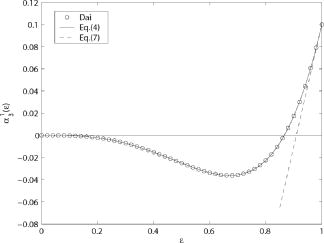

A consequence of Eq. 4 is that

Eq. 7

{\frac{\partial α_{n}^{m}}{\partial ϵ} ∣}_{ϵ = 1} = n α_{n}^{m} + 2 (n + 1) [α_{n + 2}^{m} + α_{n + 4}^{m} + \dots] .

Equation 7 shows a significant sensitivity of

α_{n}^{m} (ϵ)

when

ϵ

is slightly below its nominal value of 1, especially when high-order aberrations are present. In our example we obtain a relative sensitivity

1 ∕ α (\partial α ∕ \partial ϵ)

of 11, indicating that the NA value should be specified to

10^{- 3}

accuracy when the required coefficient accuracy is 1%.

The Strehl ratio⁴ is approximated as:

Eq. 8

S \approx 1 - \sum_{n, m} \frac{{(α_{n}^{m})}^{2}}{γ_{m} (n + 1)}

in which

γ_{0} = 1, γ_{1} = γ_{2} = \dots = 2

and the term with

n = m = 0

is omitted. A consequence of Eq. 7 is that

Eq. 9

{\frac{\partial S}{\partial ϵ} ∣}_{ϵ = 1} = 2 \sum_{n, m} \frac{{(α_{n}^{m})}^{2}}{γ_{m} (n + 1)} - 2 \sum_{m} \frac{1}{γ_{m}} {(\sum_{n} α_{n}^{m})}^{2} = 2 [\bar{{∣ Φ ∣}_{disk}^{2}} - \bar{{∣ Φ ∣}_{rim}^{2}}],

where the two averaging operations are over the whole disk

0 ⩽ ρ ⩽ 1

and the rim

ρ = 1

, respectively. Figure 2 shows the dependence on

ϵ

of the Strehl ratio in the case of a mixture of low- and high-order spherical aberration:

α_{4}^{0} = 2 π (0.02)

and

α_{6}^{0} = - 2 π (0.02)

, where the scaled Strehl ratio

S (ϵ)

is calculated by combining Eqs. 8, 4. This result compares well with the numerical calculation obtained from the lithography simulator SOLID-C.⁵ Intuitively it is expected that the Strehl ratio increases when the NA is decreased. However, in general this is not true. In the special case shown in Fig. 2, the Strehl ratio decreases when the NA is decreased from its maximum value. This result can be seen as follows: as in our example

\sum_{n} α_{n}^{m} = 0

for each

m

value, the phase aberration

Φ (1, θ)

at the rim of the pupil equals 0. From Eq. 9 it then follows that the slope at

ϵ = 1

is positive.

Fig. f2

Scaling the Strehl ratio when $α_{4}^{0} = - α_{6}^{0} = 2 π (0.02)$ . The solid line represents the combination of Eqs. 8, 4, the circles represent SOLID-C numerical calculation, and the dashed line represents the tangent line given by Eq. 9.

Appendices

Appendix A: Proof of the Main Result, Eq. 4

By decoupling per azimuthal order $m = 0, 1, \dots$ , and normalization and orthogonality⁴ of $R_{n}^{m} (ρ), n = m, m + 2, \dots$ , the Zernike coefficients $α_{n}^{m} (ϵ)$ of $Φ (ρ ϵ, θ)$ and the Zernike coefficients $α_{n}^{m}$ of $Φ (ρ, θ)$ are related by

Eq. 10

α_{n}^{m} (ϵ) = 2 (n + 1) \sum_{n^{'}} α_{n^{'}}^{m} M_{n n^{'}}^{m} (ϵ), n = m, m + 2, \dots .

The summation in Eq. 10 is over

n^{'} = m, m + 2, \dots

, and

Eq. 11

M_{n n^{'}}^{m} (ϵ) = \int_{0}^{1} R_{n}^{m} (ρ) R_{n^{'}}^{m} (ρ ϵ) ρ d ρ, n, n^{'} = m, m + 2, \dots .

We shall show that

Eq. 12

M_{n n^{'}}^{m} (ϵ) = \frac{1}{2 (n + 1)} [R_{n^{'}}^{n} (ϵ) - R_{n^{'}}^{n + 2} (ϵ)];

in particular, it follows that

M_{n n^{'}}^{m} (ϵ) = 0

when

n^{'} < n

and that

M_{n n^{'}}^{m} (ϵ)

does not depend on

m

, except that in Eq. 10 we only use

n, n^{'} = m, m + 2, \dots

. For this we use⁶

Eq. 13

R_{l}^{k} (ρ) = {(- 1)}^{(l - k) ∕ 2} \int_{0}^{\infty} J_{l + 1} (r) J_{k} (ρ r) d r, 0 ⩽ ρ < 1,

when

k, l

are integers

⩾ 0

with same parity; in the case of

k - l > 0

, the right-hand side of Eq. 13 vanishes, which is consistent with the convention that then

R_{l}^{k} \equiv 0

. We use Eq. 13 in Eq. 11 to rewrite

R_{n^{'}}^{m} (ρ ϵ)

and interchange integrals to get

Eq. 14

M_{n n^{'}}^{m} (ϵ) = {(- 1)}^{(n^{'} - m) ∕ 2} \int_{0}^{\infty} J_{n^{'} + 1} (r) [\int_{0}^{1} R_{n}^{m} (ρ) J_{m} (ρ ϵ r) ρ d ρ] d r .

To the inner integral we apply the result

Eq. 15

\int_{0}^{1} R_{n}^{m} (ρ) J_{m} (ρ v) ρ d ρ = {(- 1)}^{(n - m) ∕ 2} [\frac{J_{n + 1} (v)}{v}]

from the Nijboer-Zernike theory,⁴ and we get

Eq. 16

M_{n n^{'}}^{m} (ϵ) = {(- 1)}^{(n^{'} + n - 2 m) ∕ 2} \int_{0}^{\infty} \frac{J_{n^{'} + 1} (r) J_{n + 1} (ϵ r)}{ϵ r} d r .

Next we use the identity⁷

Eq. 17

\frac{J_{n + 1} (ϵ r)}{ϵ r} = \frac{J_{n} (ϵ r) + J_{n + 2} (ϵ r)}{2 (n + 1)},

and use Eq. 13 to rewrite the resulting two integrals in terms of Zernike polynomials. This gives Eq. 12.

Appendix B: Dai’s Formula

We reproduce Dai’s formula³ for the scaling of Zernike coefficients:

Eq. 18

α_{n}^{m} (ϵ) = ϵ^{n} [α_{n}^{m} + (n + 1) \sum_{i = 1}^{(N - n) ∕ 2} α_{n + 2 i}^{m} \sum_{j = 0}^{i} \frac{{(- 1)}^{i + j} (n + i + j)!}{(n + j + 1)! (i - j)! j!} ϵ^{2 j}]

with

N

being the maximum

n

value.

References

1.

B. J. Lin, “Signamization of resist images,” Proc. SPIE, 3051 620 –628 (1997). 0277-786X Google Scholar

2.

A. Engelen, R. Socha, E. Hendrickx, W. Scheepers, F. Nowak, M. van Dam, A. Liebchen, and D. Faas, “Optimization on step & scan systems,” Proc. SPIE, 5377 1323 –1333 (2004). 0277-786X Google Scholar

3.

G. M. Dai., “Scaling Zernike expansion coefficients to smaller pupil sizes: a simpler formula,” J. Opt. Soc. Am. A, 23 539 –543 (2006). https://doi.org/10.1364/JOSAA.23.000539 0740-3232 Google Scholar

4.

M. Born and E. Wolf, Principles of Optics, 7th ed.Cambridge University Press, Cambridge, MA (2001). Google Scholar

5.

SOLID-C (release 6.3.0), Google Scholar

6.

R. J. Noll, “Zernike polynomials and atmospheric turbulence,” J. Opt. Soc. Am., 66 207 –211 (1976). 0030-3941 Google Scholar

7.

M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, 361 Dover, New York (1970). Google Scholar

Citation Download Citation

Augustus J.E.M. Janssen and Peter Dirksen "Concise formula for the Zernike coefficients of scaled pupils," Journal of Micro/Nanolithography, MEMS, and MOEMS 5(3), 030501 (1 July 2006). https://doi.org/10.1117/1.2345672

Published: 1 July 2006

Access the abstract

JOURNAL ARTICLE
3 PAGES

DOWNLOAD PAPER SAVE TO MY LIBRARY

GET CITATION

CITATIONS

Cited by 23 scholarly publications.

Explore citations on Lens.org

RIGHTS & PERMISSIONS

Get copyright permission Get copyright permission on Copyright Marketplace

KEYWORDS

Lithography

Image processing

Monochromatic aberrations

Scanners

Zernike polynomials

Solids

Computer simulations

1.

Introduction

2.

Zernike Coefficients of Scaled Pupils

Eq. 1

Eq. 2

Eq. 3

Eq. 4

3.

Examples and Sensitivity Analysis

Eq. 5

Eq. 6

Fig. f1

Eq. 7

Eq. 8

Eq. 9

Fig. f2

Appendices

Appendix A: Proof of the Main Result, Eq. 4

Eq. 10

Eq. 11

Eq. 12

Eq. 13

Eq. 14

Eq. 15

Eq. 16

Eq. 17

Appendix B: Dai’s Formula

Eq. 18

References

Show All Keywords

Keywords/Phrases

Search In:

Publication Years