|
|
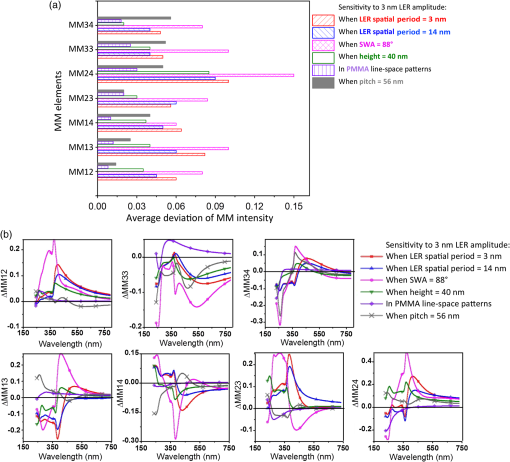
1.IntroductionThe semiconductor industry continues to drive patterning solutions that enable reduced device dimensions. With decreasing feature size, not only the line-width but also the line-shape and line edge roughness (LER) become more important. The term roughness usually denotes the deviation from a reference flat surface or from a reference straight line. The deviation from a reference flat surface of a thin film on a substrate is termed surface roughness. The deviation of the edges in a patterned structure from the mean straight line is termed LER, while the deviation from the mean line width is termed line width roughness (LWR). The LER/LWR [Fig. 1(a)] behavior must be quantified as a function of the frequency and amplitude of the LER/LWR features. The critical dimension (CD) can be used to provide a relative reference scale for the frequency of the LER/LWR features, thus defining it as high-frequency LER/LWR or low-frequency LER/LWR.1 When the wavelength of roughness that appears along the line edge is small relative to the CD, the LER is termed as high-frequency LER and conversely, when the wavelength of the roughness is large compared to the CD, the LER is characterized as low-frequency LER. The International Technology Roadmap for Semiconductors (ITRS) indicates that LER measurement and control improvements are significant industry requirements.2 LER does not scale down with the dimensions of the fabricated structures, i.e., as device dimensions go down, the magnitude of the roughness remains about the same and becomes an increasing fraction of their size which can negatively impact device performance.1 The ITRS states that LER/LWR affects dopant concentration profiles, interconnect wire resistance, gate leakage, and lowers the yield in sub-20 nm structures. Hence, characterizing wafer-to-wafer LER/LWR during lithography is the critical step in improving overall yield of the process. Fig. 1(a) Schematic definition of line edge roughness (LER) and line width roughness (LWR), (b) top down scanning electron microscope (SEM) images of 28-nm pitch Si fins acquired at four corners and center (top left, top right, center, bottom right, and bottom left) of a macro.  Optical scatterometry is one of the most prevalent inline metrology techniques in semiconductor manufacturing. Quick, nondestructive, and high-process integrability are some of the well-known advantages of optical scatterometry. Scatterometry or optical CD metrology is carried out by comparing measured spectra of the diffracted light from a periodic array of nanostructures to simulated spectra. The simulations or forward problem approach of scatterometry can be carried out using optical response simulators such as rigorous coupled-wave analysis, the finite element method, the boundary element method, or the finite-difference time-domain method. The structural profile can be extracted with the help of regression-based data analysis. This is also known as the inverse approach of scatterometry, and can be carried out with the help of linear and nonlinear regression methods wherein the structural profile is achieved through an iterative procedure that repeatedly requires computation of the forward optical modeling or with the help of a library search method, wherein an optical response library is generated prior to the measurement, and then a best-fit match with the measured spectra is determined with the help of algorithms.3 This paper demonstrates the use of Mueller matrix spectroscopic ellipsometry (MMSE)-based scatterometry for quantifying LER in directed self-assembly (DSA) patterned Si fins with the help of multiparameter scatterometry models. Although research into DSA patterning has demonstrated a high potential as a nanoscale patterning process, there are critical challenges like LER that must be overcome before transferring DSA into high-volume manufacturing. LER measurements carried out with the help of scanning electron microscope (SEM) show that the root mean-square magnitude of the LER of to 3.5 nm in DSA patterned structures and LWR in DSA patterned structures is lower than LER because the DSA edges are correlated.4 ITRS requires less than 1.8 and 1.3 nm LER in the patterned structures for 22 and 16 nm half-pitch nodes.5 A number of publications addressed the influence of LER in patterned structures on the measured optical spectra.1,6–8 LER and grating imperfections are characterized with the help of approximate effective medium approximation (EMA) models. The optical spectra contain scattered light information and can be in the form of reflectance, traditional ellipsometry parameters or Mueller matrix (MM) elements. However, Mueller measurements have better sensitivities to small structural changes and provide more information about the sample than traditional spectroscopic ellipsometry (SE) and spectroscopic reflectometry (SR) measurement.9,10 Profile reconstruction of patterned structures in scatterometry models that incorporate line roughness has been largely neglected likely because it increases the number of floating parameters and the correlation between these parameters and computation time. The multiparameter scatterometry models that include the surface roughness as demonstrated in this study can be used offline for predictive modeling and a library-based search can be carried out as a quick and effective approach for LER measurements. 2.Experimental DetailsThe wafer used in this study is from the early stages of development of a neutral layer lift off (NLLO) chemoepitaxy process. Hence, a variation in quality of Si fins is observed across the wafer. For example, the presence of LER/LWR in Si fins as observed in the top down SEM images [Fig. 1(b)], the depths of the trenches between the Si fins vary across the sample, and a layer of unetched SiN is present on top of Si fins as observed in the cross-section transmission electron microscope (TEM) image (Fig. 2). These patterning imperfections make the sample optimal for metrology testing but do not reflect the final process. MMSE-based scatterometry is used to measure the pattern imperfections. The NLLO chemoepitaxy process used in this study does produce high-quality patterns.4 Fig. 2Cross-section transmission electron microscope image of 28-nm pitch Si fins fabricated by directed self-assembly patterning. The contrast between Si fins and bulk Si region is due to amorphization of the Si fin region in the sample during sample preparation by Ga ion beam.11  Experimental MM optical spectra acquired in conical diffraction mode provides more information about the grating structure, which is very useful in decorrelating the increasing number of feature parameters. The resulting MM is seen in Eqs. (1) and (2)12 Here, Traditional ellipsometry functions; and for both planar and conical diffraction modes can be calculated from MM elements by Eq. (3).13 The scattered light intensity in parallel () and perpendicular () directions after reflection from the sample is measured in reflectometry measurements. The reflectometry functions, and can also be calculated from MM elements by Eq. (4).14 Hence, it can be said that SE and SR functions are the subsets of MM elements. Generalized ellipsometric data (all 16 Mueller elements) is collected from a square macro at azimuthal angles between 0 deg and 360 deg with a step size of 5 deg over a spectral range from 245 to 1000 nm using a J.A. Woollam RC2® spectroscopic ellipsometer. The angle of incidence for all the measurements is fixed at 65 deg to allow use of focusing probes. Focusing optics and camera are used to center the incident beam spot () inside a square macro. In order to confirm the results, MMSE data is collected at five different spots (four corners and center) of the macro. Figure 3(a) shows optical spectra of seven different MM elements at a 65 deg angle of incidence in the wavelength region of 250 to 1000 nm. Fig. 3(a) Experimental Mueller matrix spectroscopic ellipsometry (MMSE) data of individual Mueller matrix (MM) elements at 0 deg to 360 deg azimuthal angles for 65 deg incident angle. MM intensities are plotted in polar coordinates with wavelength and azimuthal angle as radial and angular coordinate, (b) schematic for azimuthal angle. 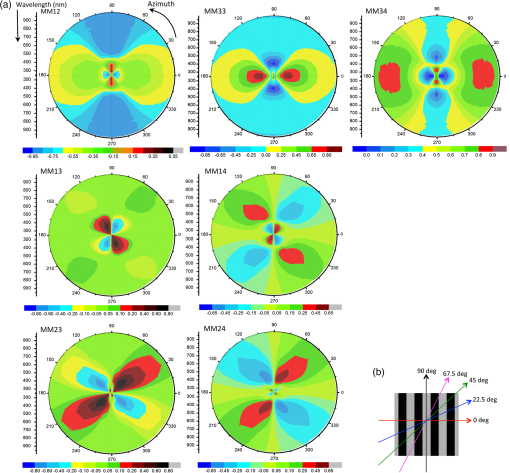 For an appropriate depiction of the anisotropic nature (structural) of the Si fin samples and its effect on MM optical spectra, the MM intensities are plotted in polar coordinates with wavelength and azimuthal angle as radial and angular coordinates, respectively. It can be observed that the highest peaks in the optical spectra of on-diagonal MM elements are observed at azimuthal angles of 0, 90, 180, and 270 deg and the highest peaks in the optical spectra of off-diagonal MM elements are at azimuthal angles of 60, 120, 240, and 300 deg, in the wavelength range of 300 to 500 nm (conical diffraction mode). However, the off-diagonal elements are zero at 0, 90, 180, and 270 deg azimuthal angles (planar diffraction mode). Hence, a 60 deg azimuthal angle is selected for sensitivity analysis. The MM for a sample is a function of the direction of propagation and wavelength (). The direction of propagation is defined by both the incidence angle and the azimuthal angle. The azimuthal angle is the angle between the grating direction and angle of incidence as seen in Fig. 3(b). For planar diffraction mode, the periodic structures are perpendicular to the plane of incidence, all diffracted orders of reflected light beam are within the plane of incidence, and cross-polarization is absent. Mirror symmetry about the incidence plane leaves the parallel components of electric fields invariant, while the perpendicular components of electric field change sign resulting in zero intensity for the off-diagonal MM elements. On the other hand, if periodic structures are not perpendicular to the plane of incidence or if there is no mirror symmetry, cross-polarization of parallel and perpendicular components of the electric field occur resulting in nonzero intensities of off-diagonal MM elements. For example, nonzero values of the off-diagonal MM elements for Si fins in the case of azimuthal angles other than 0 deg and 90 deg is seen in Fig. 3(a). This phenomenon is called conical diffraction.8 The MM measurement does not provide additional information about an isotropic sample or for an optical or structural anisotropic sample with symmetry in planar diffraction mode, when compared to the standard ellipsometry. This statement presumes that the sample has no features (roughness) or optical properties that result in significant depolarized scattering. However, in the case of conical diffraction for samples with optical (uniaxial or biaxial anisotropic samples) or structural anisotropy (symmetric patterned structures), and less ideal surfaces (rough, nonhomogenous, and so on) because of light scattering in the near specular reflection and cross-polarization effects, the off-diagonal elements of the MM are nonzero. 3.Forward Problem Approach and Sensitivity AnalysisSimulated MM optical responses for 28-nm pitch Si fins are generated by using Nanodiffract modeling software (version number: 3.4.2.378) of Nanometrics Incorporated. Sensitivity analysis is carried out by comparing the optical responses generated for a range of grating shape parameters including pitch, side-wall angle (SWA), and CD and LER feature dimensions such as frequency and width. The range is divided into discrete steps for these parameters. It has been previously reported that when LER is incorporated in a scatterometry model, the MM elements significantly change, and the higher the amplitude of the LER, the larger the impact on the MM elements.15 The changes in the MM elements with respect to increasing LER amplitude could be understood by an increase of the pseudoisotropic character of the sample i.e., the MM elements approached zero as the LER amplitude is increased. For an isotropic sample, the off-diagonal block elements are always zero independent of the wavelength and azimuthal angle. In addition, it has been reported that the individual response of all the MM elements to change in all these feature parameters such as CD (top), SWA (bottom CD), height of the Si fins, and LER is different.15 It is important to note that the SiN layer present on the top of Si fins is not incorporated in the models and only one of the parameters in the model is being varied at a time for the sensitivity analysis, as seen in Fig. 4(a). Fig. 4(a) Si fin scatterometry models with varying feature dimensions, (b) average deviation in MM intensity calculated in the wavelength range from 250 to 800 nm at 60 deg azimuthal angle for 65 deg incident angle when only one of the feature dimensions in Si fin model is varied. 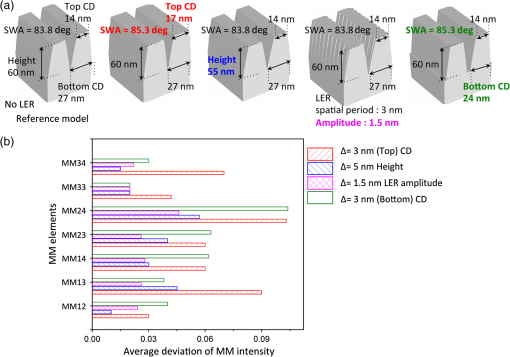 Figure 4(a) shows the average deviation of the simulated MM elements for models with varying feature dimensions with respect to the reference structure with no LER or LWR seen in Fig. 4(b). The largest response is due to a change in CD of 3 nm (bottom and top). A change in height of 5 nm results in less response, while incorporating a sinusoidal anticorrelated rectangular-shaped LER of 1.5-nm amplitude and 3-nm spatial period in the Si fin model has the least impact on the optical response of MM elements as seen in Fig. 4(a). In general, for data simulated at 60 deg azimuth, the off-diagonal elements have a higher response to variation than the on-diagonal element and the MM24 off-diagonal MM element has the highest sensitivity. The above analysis characterizes sensitivity to changes in the ideal structure. However, it is important to characterize the effect of changes in feature dimensions like spatial period of LER, SWA, height, optical properties, and pitch of line-space patterns to MM elements’ LER sensitivity. To observe the difference in response of the individual MM elements due to LER with changes in these feature parameters, the simulated optical spectra for various models with varying feature parameters and a 3-nm LER feature amplitude is subtracted from the simulated optical spectra of the same model with no LER as seen in Figs. 5(a) and 5(b). These calculated values are defined as the sensitivity of MM elements to the 3-nm LER amplitude. Fig. 5(a) Si fin scatterometry models without LER (reference models), (b) Si fin scatterometry models with LER. Feature dimensions like spatial period of LER, SWA, height, pitch, and optical properties of the fins are varied to observe their impact on LER sensitivity. 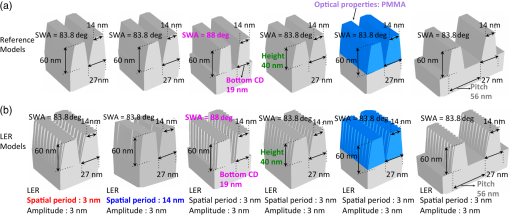 It can be observed that MM elements’ sensitivity to the amplitude of 3-nm LER features is a function of the optical properties of the material, spatial period of LER features, and pitch, height, CD, and SWA of the Si fins. The average deviations of the MM elements in the wavelength range of 250 to 800 nm obtained for a model with a 3-nm LER amplitude and varying feature parameters with respect to the undisturbed reference structure are seen in Fig. 6(a). It is observed that a high-frequency LER features (spatial period of 3 nm) has a higher impact on the calculated optical spectra of MM elements compared to a low-frequency LER (spatial period of 14 nm). Also, the sensitivity to LER increases with the height of the patterns and as the CD to pitch ratio increases. For example, the sensitivity of MM elements to LER decreases when the height of Si fins is reduced to 40 nm and the pitch value is increased to 56 nm as seen in Figs. 6(a) and 6(b). The sensitivity of MM elements to 3-nm LER features is least for the 28-nm pitch line-space patterns in which the optical properties of PMMA (photoresist material) are used instead of the optical properties of Si and is observed only in the wavelength region of 250 to 380 nm. Hence, LER inspection in photoresist line-space patterns must be carried out using a light source with ultraviolet (UV) and vacuum UV (VUV) spectral range. The highest sensitivity of MM elements to LER is observed when the SWA value is near 90 deg, i.e., when Si fins are straight and not trapezoidal. In addition, it is observed that the MM24 off-diagonal MM element has the highest sensitivity to LER for all the 28-nm pitch patterns, but on the diagonal element, MM34 is the most sensitive MM element for the Si fins with a pitch of 56 nm for data generated at a 60 deg azimuthal angle. The spectral distribution of the MM elements, more sensitivity to certain feature parameters in different wavelength regions, and different optical responses of all MM elements to change in feature parameters are helpful in separating the impact of various feature parameters like CD, height, and LER on the optical spectra during the solution of the inverse problem approach of scatterometry. 4.Inverse Problem Approach and Scatterometry ResultsThe generated optical response of the Si fin model without LER is fit to the experimentally measured optical spectra using regression-based data analysis in order to extract feature dimensions like CD, height, SWA, and line shape. The spectral and azimuthal angle dependencies of the calculated MM elements for the Si fin model with no LER agree with experimental data. However, the data fits are poor as the MM intensity of characteristic peaks for optical spectra of each MM element do not match. In scatterometry, mean squared error (MSE) is used as the criteria to estimate the degree of mismatch between experimental and model-generated MM data and is calculated from Here, is the experimental MMSE data, is the generated MMSE data, is the number of data points, and is the number of floating parameters. The difference between experimental and generated data at each azimuth, the average difference of MM intensities at each azimuth, and the MSE values obtained after the scatterometry analysis are seen in Figs. 7, 8(a), and 8(b), respectively. The average difference of experimental and generated MM intensities calculated for all azimuths is larger for the on-diagonal MM elements than off-diagonal elements because the intensity of all off-diagonal elements is very close to zero at 0 deg and 90 deg azimuthal angles as seen in Fig. 3(a). The average MM intensity difference for all off-diagonal MM elements is maximum at 60 deg azimuthal angle and for all on-diagonal MM elements is maximum at 90 deg azimuthal angle. The maximum average MM intensity difference (0.091) calculated for all azimuths from 0 deg to 180 deg is obtained for the on-diagonal MM33 element, while the maximum intensity difference is obtained for the off-diagonal element MM24 of at 60 deg and 120 deg azimuthal angles. These observations are in accord with the simulated sensitivity analysis. For example, the strongest response of change in feature dimensions and LER is observed for the MM24 off-diagonal element at 60 deg azimuthal angle. Fig. 7(a) Difference between experimental and generated MMSE data obtained after regression-based analysis for data collected at 0 deg to 180 deg azimuthal angles for 65 deg incident angle carried out with the help of reconstructed multiparameter Si fin scatterometry model without LER and (b) side view and top view of the Si fin scatterometry model without LER. 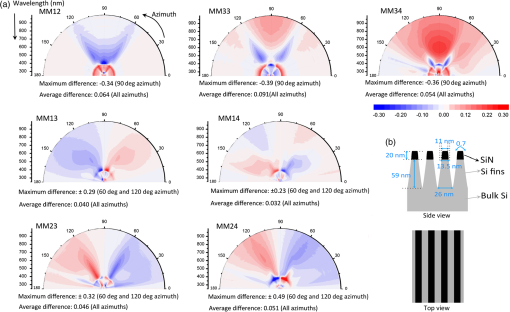 Fig. 8(a) Average MM intensity difference of individual MM elements at each azimuth from 0 deg to 90 deg azimuthal angles obtained for scatterometry model without LER and (b) MSE values obtained after regression-based analysis carried out with the help of scatterometry model without LER for data collected at azimuths from 0 deg to 180 deg. 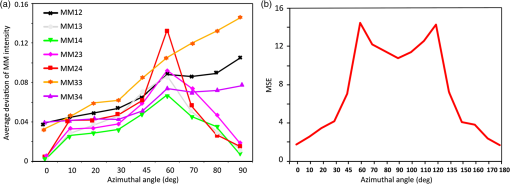 The azimuthal dependence of the MSE value is observed for the Si fin model without LER. The MSE value is least for the 0 deg azimuthal angle, increases for the subsequent azimuthal angles, and is maximum for the data collected at 60 deg azimuthal angle. MSE value decreases for data collected at 70, 80, and 90 deg azimuthal angles, but their values are still larger than the MSE obtained for data collected from 0 deg to 45 deg azimuthal angle as seen in Fig. 8(b). Large differences between fit qualities at different azimuths indicate that the model does not include critical aspects of the real structure. Hence, optimization of the scatterometry model is necessary. The azimuthal angular dependence of the MSE data obtained using the Si fin model without LER is used to diagnose the presence of pattern imperfections in the line array. Three different scatterometry models are used for the scatterometry analysis and evaluation of the LER in the Si fin samples: (a) Si fins with sidewalls having a layer with optical properties modeled using an EMA, and two multiparameter Si fin models with periodic, (b) triangular-shaped edges, and (c) rectangular-shaped edges, as seen in Figs. 9(a)–9(c), respectively. Each scatterometry model has its advantages and disadvantages. For example, the EMA-based Si fin model has the least number of floating parameters while the reconstructed profiles in the multiparameter model help in extracting an average profile of the LER features. The multiparameter model with rectangular-shaped edges can be reconstructed in such a way that LER features have correlated and anticorrelated edges. But due to software limitations, the reconstructed multiparameter model with triangular-shaped edges can only have anticorrelated edges. Fig. 9(a) Side view and top view of the effective medium approximation-based Si fin model, (b) side view and top view of the multiparameter Si fin model with triangular-shaped edges, and (c) side view and top view of the multiparameter Si fin model with rectangular-shaped edges. 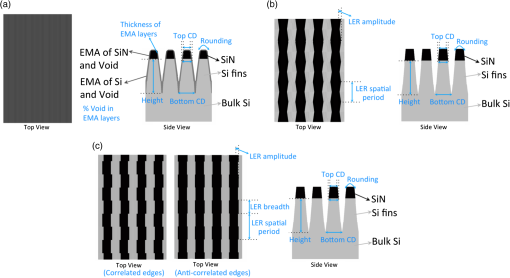 Model verification is performed by examining the difference between generated and experimental spectra as well as MSE values obtained at different azimuthal angles after model fitting. The inverse problem approach is carried out in several steps using regression-based data analysis. For example, the first step in fitting the multiparameter model is to fix the best-fit parameters for the Si fin model without LER and then add LER to that optical model. A 1-nm LER with a spatial period of 6 nm is incorporated in the Si fin model, decreasing the MSE at 90 deg azimuthal angle from 10.8 to 8.65. The LER amplitude is increased from 1 to 5 nm with a small step size of 0.5 nm. The MSE value decreased from 8.65 to 6.97 when the LER amplitude increased from 1 to 3.5 nm. Further increasing the LER amplitude increased the MSE value. Similarly, the LER spatial period is increased from 6 to 84 nm with a step size of 6 nm. The MSE value decreased from 6.97 to 5.1 when the LER spatial period dimensions increased from 6 to 48 nm, then increasing the LER spatial period value further increased the MSE value. Finally, all the parameters are allowed to float while fitting the generated data to experimental data and the least MSE is obtained for the feature parameters seen in Table 1. Table 1Floating parameters, best-fit parameters for all the scatterometry models and average mean squared error (MSE) values.
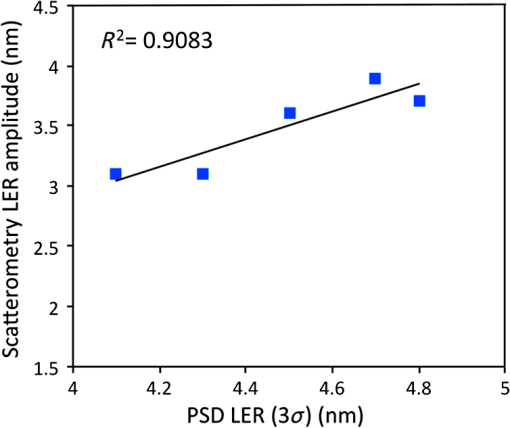
A similar approach is used for the EMA-based Si fin model and the multiparameter model (triangular-shaped edges). Incorporating LER features with correlated edges in the multiparameter model (rectangular-shaped edges) did not improve the MSE value, hence, further analysis is only carried out for the anticorrelated edges. Out of all three models, the multiparameter model (triangular-shaped edges) has the best average MSE value and its MSE value is not sensitive to change in the azimuthal angle as seen in Fig. 10. The final profile of this model and the difference in generated and experimental data are seen in Fig. 11. Fig. 10Mean squared error (MSE) values obtained for different scatterometry models at azimuths from 0 deg to 90 deg. 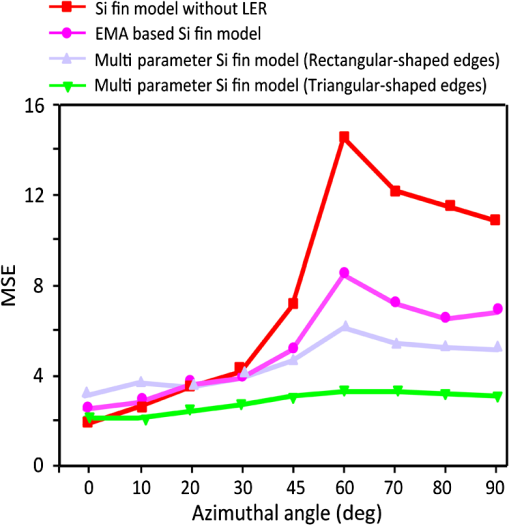 Fig. 11(a) Difference between experimental and generated MMSE data obtained after regression-based analysis for data collected at 0 deg to 180 deg azimuthal angles for 65 deg incident angle carried out with the help of reconstructed multiparameter Si fin scatterometry model (triangular-shaped edges) and (b) side view and top view of the multiparameter Si fin scatterometry model (triangular-shaped edges). 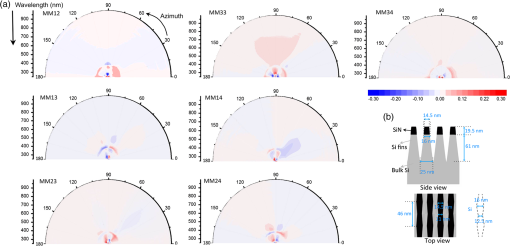 In order to validate the results obtained from scatterometry analysis, power spectral density (PSD) analysis of top down SEM images of Si fins acquired at five different positions in a macro as seen in Fig. 1 is carried out using SuMMIT software (version number: V10.12.0) of EUV Technology Corporation. For a measured edge deviation , where represents the different points along the line where the edge is measured, the spatial period behavior is analyzed by examining its Fourier transform. A convenient way of describing this frequency behavior is through the PSD, defined as the square of the magnitude of the edge deviation Fourier transform.16 A simple model for roughness correlation is to assume that very close points are perfectly correlated, and then the degree of correlation falls off exponentially with distance.16 where is the correlation function, is the distance between two points along the line, PSD is the Fourier transform of the correlation function, is the magnitude of the LER, is called the correlation length, and is called the roughness exponent.16 It is important to note that correlation length is not the average spatial period value of the LER features. The correlation length is determined from the PSD based on the effective roughness bandwidth represented by the PSD (point at which the PSD curve goes from straight to a linear-falling off-region). About 90% of the roughness is contained in periods that are longer than the correlation length and the exact fraction depends on the roughness exponent value, which is essentially a measure of the slope of the linear-falling off-region of the PSD. It has been previously reported that the PSDs of many line-space patterns (here, in each SEM image) must be averaged to reduce random errors and all three PSD parameters (, , and ) must be reported as all of them are essential for understand line-edge roughness.17,18 The advanced LER tool in SuMMIT software is used to obtain PSD LER and LWR parameters for the averaged PSD plot of all the lines in the SEM image. The PSD LER and LWR parameters for each SEM image acquired at five different positions in a macro are seen in Table 2. An SEM image acquired at the center of the macro, its PSD LER plot (average of all lines), and its PSD LWR plot (average of all lines) are shown in Figs. 12(a)–12(c), respectively. The correlation plot of LER values acquired from scatterometry analysis and PSD analysis of MMSE data and SEM images, respectively, acquired at five different positions (four corners and center) in a macro, is seen in Fig. 13.Table 2LER results obtained from PSD and scatterometry analysis.
5.Summary and ConclusionsSimulations of Si fin structures show that MM ellipsometry for the conical diffraction mode is more sensitive to the feature details of Si fins than MM ellipsometry for planar diffraction or classical SE. Feature dimensions such as top and bottom CD, line-shape, pitch, SWA, height as well as LER influence the MM elements’ response. Also, the sensitivity of MM elements is a function of the optical properties of the material, frequency of LER/LWR features, and pitch, height, CD, and SWA of the Si fins. MM elements’ sensitivity to LER increases when the CD to pitch ratio of the line-space patterns increases, height of line-space patterns increases and when SWA value of the fins is near 90 deg, i.e., when Si fins are straight and not trapezoidal. Also, the materials’ optical properties affect the sensitivity of MM elements to LER. Sensitivity to LER in the photoresist line-space patterns is less than that of LER in the Si fins. MM coefficients in the UV and VUV spectral ranges are more sensitive to feature dimensions of photoresist line-space patterns as shorter wavelength are more sensitive to nanoscale changes in LER and the photoresist materials start absorbing light in this wavelength range. The Mueller spectrum taken at each individual azimuth is sufficient to reconstruct the profile by fitting data with a simple model, but data acquired at different angles of incidence and azimuthal angles provide more information and build a more robust scatterometry model. For example, the intensity difference between the experimental and generated data is least at 0 deg azimuth for the Si fin model without LER, but scatterometry analysis and MSE values obtained at different azimuthal angles showed that optimization of the scatterometry models is necessary. Reconstructed scatterometry models can be used to characterize LER in Si fins as well as photoresist line space patterns. All the reconstructed scatterometry models had lower average MSE values than that obtained for the Si fin model without LER. This investigation shows that the off-diagonal MM elements in conical diffraction mode provide additional nonredundant information about Si fin structures that aids in model fitting. The final profile of the reconstructed scatterometry model extracted a low-frequency LER with a 46-nm spatial period with an amplitude of 3.6 nm in Si fin samples. Although the MSE values obtained using a multiparameter Si fin model (triangular-shaped edges) did not change with azimuthal angle, the average MSE value of 2.81 is a little higher than the expected MSE values. This is attributed to the use of periodic LER features and the models’ inability to incorporate the varying height of Si fins as seen in its TEM image. Optimizing features like correlated or anticorrelated edges, unevenness in the height of the Si fins across the sample, and using multiple spatial period edges in the multiparameter model to get better data fits and lower-MSE values is one of the future goals. Various numerical methods can be used to generate rough edges, surfaces, and volumes that follow the specific PSD parameters of sigma, roughness exponent, and correlation length obtained from PSD analysis of top down images of Si fin samples.19 These specific rough edges, whether correlated or anticorrelated edges with different spatial periods, will be incorporated in the scatterometry models with a much larger field of view. The inverse problem approach in this work is time consuming as it is carried out with the help of linearized regression-based data analysis. LER inspection is carried out offline after the sample is prepared. Reconstructed scatterometry models demonstrated in this work to quantify LER must be used to generate data offline and a library-based search should be carried out as a quick and effective approach for LER measurements in industry, where the size of the library is not a concern and the general profile is known beforehand. In addition, an algorithm can be prepared on the basis of the difference in generated data and experimental data and used in the in-line control method that could monitor and alarm when the LER appears above a certain level. AcknowledgmentsWe acknowledge funding from the SRC. We are thankful to GlobalFoundries and Nanometrics Inc. for the help with scatterometry modeling and analysis. We would also like to acknowledge the support and guidance provided by Dr. Richard Farrell (TEL). ReferencesB. Yaakobovitz, Y. Cohen and Y. Tsur,
“Line edge roughness detection using deep UV light scatterometry,”
Microelectron. Eng., 84
(4), 619
–625
(2007). http://dx.doi.org/10.1016/j.mee.2006.12.002 MIENEF 0167-9317 Google Scholar
“The international technology roadmap for semiconductors,”
(2015) http://www.itrs.net/ITRS%201999-2014%20Mtgs,%20Presentations%20&%20Links/2013ITRS/Summary2013.htm July ). 2015). Google Scholar
X. Chen et al.,
“Improved measurement accuracy in optical scatterometry using fitting error interpolation based library search,”
Appl. Opt., 52
(27), 6726
–6734
(2013). http://dx.doi.org/10.1364/AO.52.006726 APOPAI 0003-6935 Google Scholar
G. Schmid et al.,
“Fabrication of 28nm pitch Si fins with DSA lithography,”
Proc. SPIE, 8680 86801F
(2013). http://dx.doi.org/10.1117/12.2011607 PSISDG 0277-786X Google Scholar
P. Naulleau, A. George and B. McClinton,
“Mask roughness and its implications for LER at the 22 and 16nm nodes,”
Proc. SPIE, 7636 76362H
(2010). http://dx.doi.org/10.1117/12.851561 PSISDG 0277-786X Google Scholar
A. Heinrich et al.,
“Application of Mueller matrix spectroscopic ellipsometry to determine line edge roughness on photomasks,”
Proc. SPIE, 8886 88860L
(2013). http://dx.doi.org/10.1117/12.2030627 PSISDG 0277-786X Google Scholar
M. Foldyna, T. Germer and B. Bergner,
“Mueller matrix ellipsometry of artificial non-periodic line edge roughness in presence of finite numerical aperture,”
Proc. SPIE, 7971 79710N
(2011). http://dx.doi.org/10.1117/12.879518 PSISDG 0277-786X Google Scholar
B. Bergner, T. Germer and T. Suleski,
“Effect of line width roughness on optical scatterometry measurements,”
Proc. SPIE, 7272 72720U
(2009). http://dx.doi.org/10.1117/12.813770 PSISDG 0277-786X Google Scholar
T. Novikova et al.,
“Application of Mueller polarimetry in conical diffraction for critical dimension measurements in microelectronics,”
Appl. Opt., 45
(16), 3688
–3697
(2006). http://dx.doi.org/10.1364/AO.45.003688 Google Scholar
G. Muthinti et al.,
“Mueller based scatterometry measurement of nanoscale structures with anisotropic in-plane optical properties,”
Proc. SPIE, 8681 86810M
(2013). http://dx.doi.org/10.1117/12.2011649 PSISDG 0277-786X Google Scholar
J. McCaffrey, M. Phaneuf and L. Madsen,
“Surface damage formation during ion-beam thinning of samples for transmission electron microscopy,”
Ultramicroscopy, 87
(3), 97
–104
(2001). http://dx.doi.org/10.1016/S0304-3991(00)00096-6 ULTRD6 0304-3991 Google Scholar
T. Harland and E. Irene, Handbook of Ellipsometry, William Andrew, New York
(2005). Google Scholar
D. Ramsey and K. Ludema,
“The influences of roughness on film thickness measurements by Mueller matrix ellipsometry,”
Rev. Sci. Instrum., 65
(9), 2874
–2881
(1994). http://dx.doi.org/10.1063/1.1144631 RSINAK 0034-6748 Google Scholar
S. Yaoming et al.,
“Spectral sensitivity analysis of OCD based on MM formulism,”
ECS Trans., 34
(1), 955
–960
(2011). http://dx.doi.org/10.1149/1.3567698 Google Scholar
D. Dixit et al.,
“Silicon fin line edge roughness determination and sensitivity analysis by Mueller matrix spectroscopic ellipsometry based scatterometry,”
Proc. SPIE, 9424 94242O
(2015). http://dx.doi.org/10.1117/12.2185543 PSISDG 0277-786X Google Scholar
C. Mack,
“Measuring line edge roughness: fluctuations in uncertainty,”
(2015) http://www.lithoguru.com/scientist/litho_tutor/Tutor62%20(Aug%2008).pdf July ). 2015). Google Scholar
C. Mack,
“More systematic errors in the measurement of power spectral density,”
Proc. SPIE, 9424 942403
(2015). http://dx.doi.org/10.1117/12.2085025 PSISDG 0277-786X Google Scholar
C. Mack,
“Understanding the efficacy of linewidth roughness post-processing,”
Proc. SPIE, 9425 94250J
(2015). http://dx.doi.org/10.1117/12.2085047 PSISDG 0277-786X Google Scholar
C. Mack,
“Generating random rough edges, surfaces, and volumes,”
Appl. Opt., 52 1472
–1480
(2013). http://dx.doi.org/10.1364/AO.52.001472 APOPAI 0003-6935 Google Scholar
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||