|
|
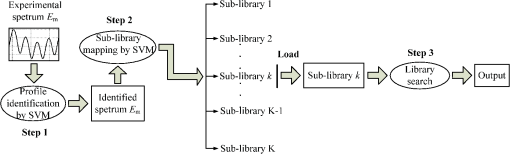
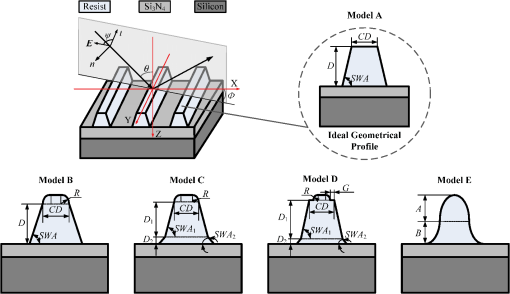
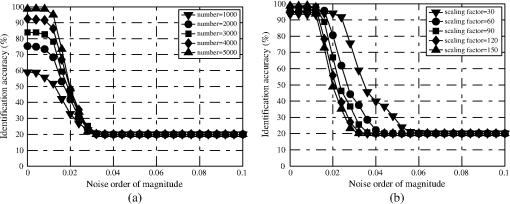
1.IntroductionOptical scatterometry is a noncontact, nondestructive, and accurate technique that is now widely used in the reconstruction of geometrical profiles for semiconductor structures.1,2 Generally, two procedures are required in this technique. The first one involves simulation of the optical signature from a diffraction structure using reliable forward modeling techniques, such as rigorous coupled-wave analysis (RCWA),3,4 the boundary element method,5 or the finite-difference time-domain method.6 The second procedure involves the reconstruction of the semiconductor structures from the measured signatures, which is a typical inverse problem. To solve the inverse problem in optical scatterometry, several approaches have been reported in recent years. Drège et al. presented a linear approach to obtain surface profile information by the linearized inversion of scatterometric data.7 Since a highly nonlinear relationship exists between the optical signature and the profile parameters, the linear approach has its inherent limitations. Some nonlinear optimization approaches, such as the Levenberg-Marquardt (LM) algorithm and its improved technique by combining with artificial neural network (ANN), have also been proposed.8–10 The optimization approach is usually time-consuming, as the structural profile is achieved through an iterative procedure that repeatedly requires computation of the forward optical modeling. This is even worse and unacceptable when dealing with two-dimensional structures or more complex structures. Most recently, Jin et al. reported a support vector machine (SVM) based method,11 in which the measured diffraction signatures were inputted into a trained SVM to directly obtain the values of profile parameters as outputs. Although it is quite similar to the ANN-based method,12,13 the SVM-based method can to some extent achieve an optimal result under conditions of limited information. This is because ANN is based on the principle of experience risk minimization while SVM is a machine learning algorithm based on statistical learning theory (SLT).14,15 Consequently, the SVM-based method can obtain a better generalization performance.16–18 The library search has been developed for several decades and has been demonstrated to be an effective approach to solve the inverse problem in optical scatterometry.19 Due to the robustness and convenience of this method, it is commonly used in industry. In a library search, a signature library is built up in advance by using different combinations of profile parameters, and the experimental signature is compared with the library for the best match. Before building the signature library, the geometrical model of the structure is often assumed to be known, and then the signatures in the library are simulated using forward modeling techniques from the model. However, there exists an issue when a wrong model is used, i.e., the real geometrical profile of a structure is quite different from the geometrical model used in the forward modeling, the solution to the inverse problem will lead to an inaccurate or erroneous result. Another issue in library search is the fast and accurate search of a simulated signature for a measured one when the signature library grows increasingly large. Seeking for the most similar simulated signature in a library for a measured one is a typical nearest neighbor search problem.20 Currently, most of the efforts to solve this problem are made by developing efficient search algorithms with an emphasis on matching accurately and rapidly. Although some typical search algorithms such as the linear search and k-dimensional (k-d) tree search can ensure an exact result,21,22 the search time is usually unacceptable when the library is very large. The locality-sensitive hashing (LSH) is another kind of method to improve the search speed,23 but as a randomized algorithm, it does not guarantee an exact result but guarantees a high probability for a correct result or one close to it. In addition to developing efficient search algorithms, it is highly desirable to reduce the search space of the library to as small as possible. In this paper, we propose an SVM-based method to deal with two issues in library search for optical scatterometry. For the first issue, the identification of geometrical profile, we generate an SVM classifier whose input denotes the optical signature and the output denotes its corresponding geometrical model. For the second issue, the fast search of simulated signature for the measured one in the signature library, we also generate another set of several SVM classifiers to divide the large library into many small sublibraries. In the sublibrary, we can use some traditional search algorithms, such as linear search and k-d tree search methods, to accurately search for the optimal simulated signature. Though similar in some aspects to the pioneering work reported in Ref. 11, there are two main concepts in this paper, namely, the identification of geometrical profiles (i.e., the selection among geometrical models) by SVM and the fast extraction of geometrical parameters by adding SVM into the traditional search method. As a sublibrary is only a part of the whole library, the search in the small range would be much faster than in the whole library. It is also possible to further increase the search speed by dividing the whole library into more sublibraries and training the corresponding new SVM classifiers, and this becomes important and meaningful when the whole library is huge and the hardware resources are limited. The remainder of this paper is organized as follows. Section 2 introduces the principle of SVM, and then describes the SVM-based library search strategy in detail. Section 3 provides some simulation and experimental results to verify the proposed SVM method. Finally, we draw some conclusions in Sec. 4. 2.Theory2.1.Principle of SVMSVM was originally designed to solve the binary classification problem, and the key of SVM is its kernel function.13 By using a proper kernel function, we can nonlinearly map the input signatures to a high-dimensional feature space. Then, in the high-dimensional feature space, we can construct an optimal separating hyperplane so that we can classify those signatures. For a binary classification problem, the training pairs are represented as where is an -dimensional vector representing the th training signature, is a scalar with two values of and 1 representing two classes, and is the number of training pairs. The training pairs are used in the training of an SVM classifier.For a measured signature , the value of a decision function determines which class belongs to. The decision function can be expressed as where is a mapping function of , is a bias, and is a support vector that can be expressed as a linear combination of : where is the weight coefficient of the th input signature. By substituting Eq. (3) into Eq. (2), and by defining a new function we can get the final expression of the decision function asThe function in Eqs. (4) and (5) is called the kernel function, which plays an important role in SVM. Several kernel functions, such as the linear kernel, polynomial kernel, Sigmoid kernel, and radial basis function (RBF) kernel have been applied in SVM to suit for different situations. Different kernel functions have different adjustable parameters, which may have different influence on the final classification result for SVM. In this paper, we choose the RBF as the kernel of all the SVMs used in the identification of geometrical profiles and in the SVM-based library search. The RBF kernel is expressed as where the scaling factor is the adjustable parameter, and represents the 2-norm.It should be pointed out that SVM was originally designed to solve the binary classification problem, but most of the classification problems can be attributed to a multiclassification one. Recently, researchers have developed several multiclassification SVM algorithms such as “one-against-all,” “one-against-one,” and directed acyclic SVM.24 In this paper, we simply use the support vector machines tool for multiclassification developed by Chang and Lin.25 2.2.SVM-Based Library Search StrategyIn this paper, we divide the reconstruction of diffraction structures by the SVM-based library search into three steps, as shown in the flowchart of Fig. 1. The first step is the identification of the geometrical profile model for a diffraction structure by its measured optical signature . Then in the second step, the measured signature with its profile model identified is mapped into a sublibrary that is a subset of the whole signature library. Finally, in the third step, a search algorithm is used to find the most similar simulated signature for the measured signature . For the first step, an SVM classifier is used to identify the geometrical profile of a structure by its measured optical signature. The SVM classifier is trained off-line in advance, and training pairs should be prepared for the training. Then testing pairs are inputted into the trained SVM classifier to test its identification accuracy. Here we define the identification accuracy as the number of the correctly identified testing pairs divided by the total number of testing pairs. For the generation of training pairs, we translate the profile information of each structure into a numeric form. Supposing that there are possible geometrical profiles caused by the process variations of semiconductor fabrication for an ideal trapezoidal grating, and the possible geometrical profile in the profiles is represented by a unique numeric “”. This means that the number of output classes of the SVM classifier is the same as the number of the geometrical profiles. In the case of the -profiles identification problem, the total training pairs are composed of a mixture of subsets. The subset in the subsets contains a number of pairs calculated from geometrical parameters of the profile in a defined variation range, and each training pair is composed of the optical signature and the unique numeric “” designating the geometrical profile . After selection of the kernel function and preparation of training pairs, we train the SVM classifier to produce numeric “” for every optical signature of the geometrical profile . Once the training stops, the trained SVM classifier can be used to identify the geometrical profiles of structures, i.e., to select the geometrical models. In the second step, the measured signature with its profile model identified is mapped into a sublibrary by another set of several trained SVM classifiers. The sublibrary is a subset of the whole signature library that is commonly used in the traditional library search method. As there are possible geometrical profiles for the measured signature , we establish signature libraries in advance for the profiles, respectively, and each signature library is divided into several sublibraries. Before mapping the measured signature into its corresponding sublibrary, we need to perform three substeps off-line in advance, including (1) the division of variation ranges of geometrical parameters, (2) the establishment of sublibraries, and (3) the training of SVM classifiers. In the substep 1 as shown in Fig. 2, we take three geometrical parameters, namely, critical dimension (CD), depth, and sidewall angle (SWA) into account. The variation range of each geometrical parameter represented by a long rectangular is divided into two subranges, and each subrange is represented by a short rectangle with a unique color. Then we select a subrange from the range of each geometrical parameter to form a set of subranges, thus we have eight sets of subranges total as shown in the large ellipse in Fig. 2. Here we only take the binary division as an example, but actually, the number of subranges is a user-defined variable. The substep 2 involves the establishment of each sublibrary based on its corresponding set of subranges. We generate a series of discrete values equidistantly for each subrange, and then we select three values in total from each of the subranges of CD, depth, and SWA to completely characterize the trapezoidal grating. Finally, we generate the simulated diffraction signature for the selected set of values of geometrical parameters and store it in the sublibrary. We can establish the whole sublibrary by repeatedly choosing a different set of discrete values of geometrical parameters in the set of subranges, and following this, all the sublibraries can be established. The substep 3 is to train the SVM classifiers by generating training pairs. We generate three SVM classifiers with each one corresponding to a geometrical parameter, as there are three geometrical parameters to be extracted. Since the range of each parameter is divided into several subranges, its corresponding classifier has several classes with each one corresponding to a different subrange. The optical signatures are generated by randomly varying the values of geometrical parameters in the ranges of geometrical parameters for each class. We combine the optical signatures and their corresponding class to form the training pairs and to train each SVM classifier. Once all the SVM classifiers are generated and trained off-line, we will use them to quickly map the measured signature of a trapezoidal grating to its corresponding sublibrary. Fig. 2The division of variation ranges of geometrical parameters for generating a set of SVM classifiers and sublibraries. 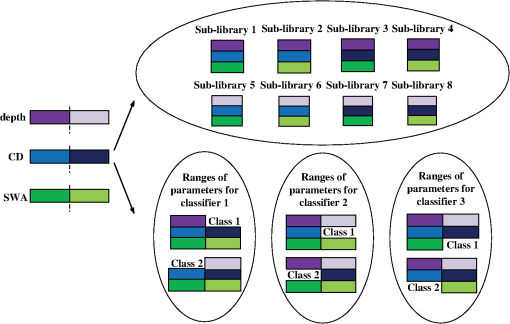 Finally in the third step, we simply use some search algorithms to find the most similar simulated signature for the measured signature in the mapped sublibrary. We can use a typical search algorithm, such as the linear search method or the k-d tree method, to search for the nearest neighbor of the measured signature . The search in the sublibrary is expected to be much faster than in the whole library, as the sublibrary is designed as a part of the whole library. 3.Results3.1.Description of the Grating ModelsFor the purpose of identification of geometrical profiles and fast extraction of geometrical parameters, simulations and experiments were conducted on a one-dimensional grating structure. In our simulations, five profile models were used, as shown in Fig. 3. The ideal one was a one-dimensional trapezoidal photoresist grating with a period of 400 nm deposited on a silicon substrate that was coated with an anti-reflective layer. This was defined as Model A with three geometrical parameters, including the top CD, depth , and sidewall angle SWA. Four other profile models, shown as Model B to Model E in Fig. 3, were used to describe the real geometrical profiles that deviated from the ideal one because of the process variations in lithography. Compared to Model A, a parameter defining the top rounding was added in Model B. The bottom footing was also considered in Model C, which was represented by six geometrical parameters. In model D, the lateral offset expressed by was further taken into account. Model E was an extreme case for a sinusoidal profile with only two geometrical parameters and , respectively defining the amplitude of the sinusoidal grating and the offset between the middle and the bottom of the profile. 3.2.Simulations for Identification of Geometrical ProfilesWe performed simulations to test the capability of the proposed SVM method in the identification of geometrical profiles, i.e., in the selection among profile models. The five profile models as shown in Fig. 3 were used for testing. We first generated the training pairs by randomly choosing values of the geometrical parameters in the following variation ranges: ; ; ; ; ; ; ; ; ; ; and . We then trained the SVM classifier using the training approach discussed above in Sec. 2.2. Once the SVM classifier was successfully trained, another set of testing pairs of optical signatures were randomly generated in the same ranges and were used to test the trained SVM classifier. The in-house forward modeling software based on RCWA was applied to simulate the optical signatures for spectroscopic elliposometry, with the incidence angle fixed at 65 deg and the wavelength varied between 380 nm and 780 nm by an increment of 10 nm. The scaling factor in the RBF kernel shown in Eq. (6) plays an important role in the performance of SVM, thus it should be carefully tuned to the problem at hand. If it is overestimated, the exponential will behave almost linearly and the higher-dimensional projection will start to lose its nonlinear power. Otherwise, if it is underestimated, the function will lack regularization, and the decision boundary will be highly sensitive to noise in training data. Therefore, we first performed particular simulations to estimate the effects of the scaling factor and the number of training signatures on the identification accuracy. For each profile model, we randomly generated 250 testing pairs of optical signatures, thus we had totally 1250 testing pairs. The simulation results for such a test are shown in Fig. 4. Fig. 4The identification accuracy varies with (a) the number of training pairs and (b) the scaling factor in the RBF kernel. 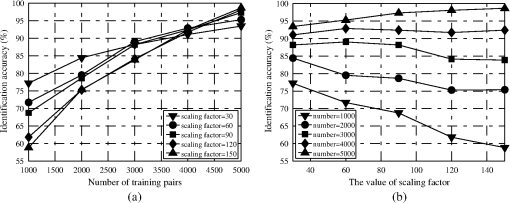 From Fig. 4(a), it is clear that for all five different values of scaling factor , the identification accuracy increases with the number of training pairs increasing, and this increasing trend is more obvious when the scaling factor becomes larger. As expected, the scaling factor does play an important role in the identification accuracy. When the number of training pairs is small, e.g., being 1000, the larger the scaling factor is, the smaller the identification accuracy becomes. However, when the number of training pairs becomes large enough, e.g., being 5000, a larger value of the scaling factor achieves a higher identification accuracy. Again in Fig. 4(b), we can easily find that the identification accuracy increases with the number of training pairs increasing for each given scaling factor. It is also interesting to note that the identification accuracy usually decreases with the scaling factor, except when the number of training pairs becomes very large. All these simulations indicate that for a given scaling factor, the number of training pairs should be carefully selected as well, so that the highest identification accuracy can be obtained. In our simulations, an optimal combination of the scaling factor and the number of training pairs is 150 and 5000, respectively. The measurement noise is also an important factor to influence the performance of the SVM classifier. Therefore, we performed another set of simulations by adding Gaussian noise into the testing signatures. Here the noise order of magnitude was defined as the ratio of the standard deviation of the added Gaussian noise to the mean value of the simulated signatures.26 Figure 5 depicts the simulation results, with the scaling factor fixed as 150 in Fig. 5(a) and the number of training pairs fixed as 5000 in Fig. 5(b). It is expected from Fig. 5 that the identification accuracy decreases with the noise order of magnitude increasing. It is also interesting to note that for each given number of testing pairs shown in Fig. 5(a) and for each given scaling factor shown in Fig. 5(b), there is always a range of the noise order where the identification accuracy remains the highest. The identification accuracy does not drop remarkably until the noise order becomes large enough to be beyond this range. This means that the identification accuracy is not so sensitive to noise in this range, which is hence called the noise-insensitive range with the noise order from zero to a very small value. Once the noise order further increases, the identification accuracy starts to decrease sharply and finally reaches a stable small value of 20%. This is because all the testing signatures are classified to Model E when the noise order is larger than a specific value. Furthermore, from Fig. 5 we can observe that the highest identification accuracy in the noise-insensitive range increases with either the scaling factor or the number of testing pairs increasing. This indicates that the larger the scaling factor or the number of testing pairs is, the less sensitive to noise the corresponding trained SVM classifier becomes. 3.3.Simulations for Extraction of Geometrical ParametersWe next continued our simulations to apply the SVM-based library search strategy in the extraction of geometrical parameters from optical signatures. Only the trapezoidal grating with three geometrical parameters , CD, and SWA was taken as an example to demonstrate the extraction process. The variation ranges for the three geometrical parameters are the same as in Sec. 3.2. We generated two different sets of sublibraries to verify the proposed SVM method. One contained four sublibraries with two SVM classifiers, and the other eight sublibraries with three SVM classifiers. For the library search strategy with two SVM classifiers, both the ranges of CD and SWA were divided into two subranges except . For the library search strategy with three SVM classifiers, all the ranges of , CD, and SWA were divided into two subranges. We then applied the proposed method to establish the sublibraries and to train the SVM classifiers. The number of training pairs for each class was chosen as 5000, the scaling factor used in the RBF kernel was set to 150, and the increments for , CD and SWA to generate the optical signatures were 0.5 nm, 0.5 nm, and 0.2 deg, respectively. Once the SVM classifiers were trained off-line successfully, we generated another set of testing pairs by adding Gaussian noise with noise order of magnitude 0.001 to the testing optical signatures. The errors of extracted parameters and the search time by the SVM-based library search strategy were compared with those by the linear search method in the whole library. The simulation results are shown in Figs. 6Fig. 7Fig. 8 to 9, and the 3 errors of extracted parameters by the linear search and by the SVM-based method with different numbers of sublibraries are summarized in Table 1. We can observe that the errors of extracted parameters by the two different methods are in the same magnitude when the initial condition was set properly. In Fig. 7, the search speed by the SVM-based method with two classifiers is at least four times faster than that by the linear search. And in Fig. 9, the search speed by the SVM-based method with three classifiers is even faster, i.e., it is at least eight times faster than that by the linear search. It thus has demonstrated that the proposed SVM-based library search strategy is not only accurate enough, but also speed-controllable. Fig. 6The search time and extracted errors of depth, CD, and SWA by (a) the linear search method and (b) the SVM-based method (with four sublibraries and two classifiers). 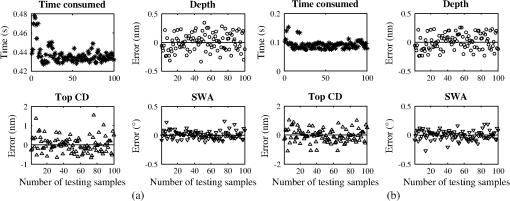 Fig. 7The comparison of search time. (a) The time consumed for the linear search method and the SVM-based method and (b) their ratio (with four sublibraries and two classifiers). 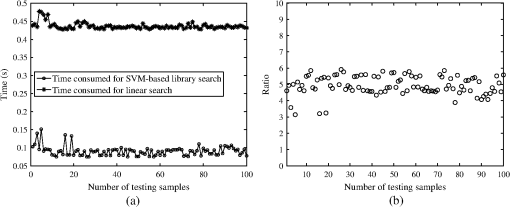 Fig. 8The search time and extracted errors of depth, CD, and SWA by (a) the linear search method and (b) the SVM-based method (with eight sublibraries and three classifiers). 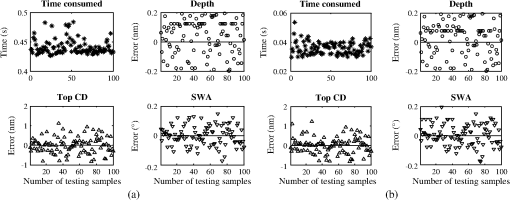 Fig. 9The comparison of search time. (a) The time consumed for linear search method and SVM-based method and (b) their ratio (with eight sublibraries and three classifiers). 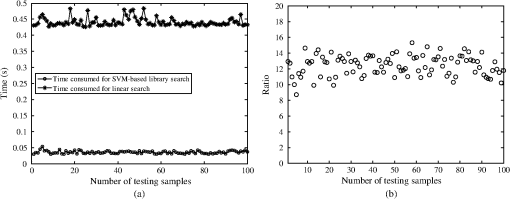 Table 13σ errors of extracted parameters by the linear search and the SVM-based methods.
3.4.ExperimentsWe performed experiments on a dual-rotating-compensator ellipsometer (RC2 ellipsometer, J. A. Woollam Co.) to validate the proposed SVM-based library search strategy. The wavelengths available were in the range of 193 to 1690 nm including the range of 380 to 780 nm used in this paper, and the incidence angle was fixed at 65 deg. We obtained and used the ellipsometric parameters as optical signatures of the measured sample. As shown in Fig. 10, the measured sample is a one-dimensional trapezoidal photoresist grating with a profile model characterized by three geometrical parameters of depth, CD, and SWA. The CD was 172 nm as measured by scanning electron microscopy. Fig. 10The one-dimensional trapezoidal photoresist grating sample under measurement. (a) The profile model and (b) the top-down scanning electron microscopy view. 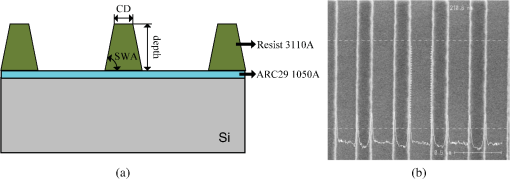 We repeatedly measured the grating sample 10 times as different measurements might contain different noise levels. Then we input the measured signatures one by one into the trained SVM classifier as described in Sec. 3.2 to identify their geometrical profiles (i.e., to select their profile models). Note that for training the SVM classifier, the values of the bottom footing , the top rounding , and the lateral offset were all set between 10 nm and 50 nm, which means that any grating profile with , , and less than 10 nm should be identified as Model A. From this point of view, all the 10 measured signatures were correctly classified to Model A, indicating that the fabricated grating sample was very close to an ideally trapezoidal profile with the bottom footing, the top rounding, and the lateral offset being too small to be considered. Once the geometrical profile of the grating sample was identified to be Model A, we finally applied a set of three SVM classifiers with eight sublibraries as described in Sec. 3.3 to extract the geometrical parameters. Here for the experiments, the increments of depth, CD, and SWA used in the establishment of sublibraries were set to 1 nm, 1 nm, and 0.1 deg, respectively. Figure 11 is a comparison of the simulated and measured signatures for the best match in one measurement with the extracted depth, CD, and SWA being 303 nm, 162 nm, and 87.6 deg, respectively. Table 2 depicts the comparison of all the extracted results by the SVM-based library search and the linear search methods. It is clear that all the extracted results by the two methods are the same, but the search time by the SVM-based method is only about 10% of that by the linear search method. Therefore, it has demonstrated that the SVM-based library search strategy is a fast and accurate method that can be applied in the reconstruction of diffraction structures. Fig. 11Comparison of the simulated and measured signatures in one of the 10 measurements for the ellipsometric parameters (a) log[tan()] and (b) cos(). 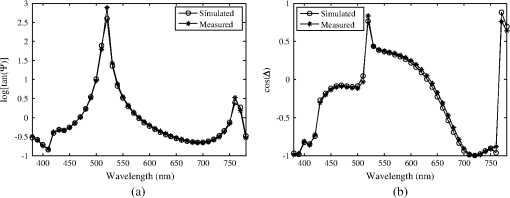 Table 2Comparison of the linear search and the SVM-based library search methods.
4.ConclusionsIn this paper, we have introduced the SVM method to deal with two issues in the identification and reconstruction of diffraction structures. For the first issue, which is the identification of the geometrical profiles, we generate an SVM classifier to map an optical signature to its corresponding geometrical profile. Our simulations and experiments have shown that the SVM classifier can accurately identify the geometrical profile of one-dimensional trapezoidal grating even though some noise exists in the signatures. For the second issue, which is the fast search of simulated signature for the measured one in the signature library, we proposed an SVM-based library search strategy. Several multiclassification SVM classifiers are trained off-line, and then they are used to map the measured signature into its corresponding sublibrary. By searching in the sublibrary, the search time can be reduced dramatically compared to the linear search in the whole library. The simulations and experiments have demonstrated that the SVM-based library search strategy can achieve a robust and fast extraction of structural parameters. AcknowledgmentsThis work was financially supported by the National Natural Science Foundation of China (Grant Nos. 91023032, 51005091, and 51121002) and the National Instrument Development Specific Project of China (Grant No. 2011YQ160002). ReferencesC. J. Raymond,
“Scatterometry for semiconductor metrology,”
Handbook of Silicon Semiconductor Metrology, 477
–514 Marcel Dekker Inc., New York
(2001). Google Scholar
C. J. Raymondet al.,
“Multiparameter grating metrology using optical scatterometry,”
J. Vac. Sci. Technol., 15
(2), 361
–368
(1997). http://dx.doi.org/10.1116/1.589320 JVSTAL 0022-5355 Google Scholar
M. G. MoharamE. B. GrannD. A. Pomment,
“Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings,”
J. Opt. Soc. Am. A, 12
(5), 1068
–1076
(1995). http://dx.doi.org/10.1364/JOSAA.12.001068 JOAOD6 0740-3232 Google Scholar
W. LeeF. L. Degertekin,
“Rigorous coupled-wave analysis of multilayered grating structures,”
J. Lightw. Technol., 22
(10), 2359
–2363
(2004). http://dx.doi.org/10.1109/JLT.2004.833278 JLTEDG 0733-8724 Google Scholar
Y. NakataM. Kashiba,
“Boundary-element analysis of plane-wave diffraction from groove-type dielectric and metallic gratings,”
J. Opt. Soc. Am. A, 7
(8), 1494
–1502
(1990). http://dx.doi.org/10.1364/JOSAA.7.001494 JOAOD6 0740-3232 Google Scholar
H. Ichikawa,
“Electromagnetic analysis of diffraction gratings by the finite-difference time-domain method,”
J. Opt. Soc. Am. A, 15
(1), 152
–157
(1998). http://dx.doi.org/10.1364/JOSAA.15.000152 JOAOD6 0740-3232 Google Scholar
E. DrégeJ. ReedD. Byrne,
“Linearized inversion of scatterometric data to obtain surface profile information,”
Opt. Eng., 41
(1), 225
–236
(2002). http://dx.doi.org/10.1117/1.1416850 OPEGAR 0091-3286 Google Scholar
H. T. HuangW. KongF. L. Terry,
“Normal-incidence spectroscopic ellipsometry for critical dimension monitoring,”
Appl. Phys. Lett., 78
(25), 3983
–2985
(2001). http://dx.doi.org/10.1063/1.1378807 APPLAB 0003-6951 Google Scholar
J. M. Holdenet al.,
“Normal-incidence spectroscopic ellipsometry and polarized reflectometry for measurement and control of photoresist critical dimension,”
Proc. SPIE, 4689 1110
–1121
(2002). http://dx.doi.org/10.1117/12.473439 PSISDG 0277-786X Google Scholar
C. W. Zhanget al.,
“Improved model-based infrared reflectrometry for measuring deep trench structures,”
J. Opt. Soc. Am. A, 26
(11), 2327
–2335
(2009). http://dx.doi.org/10.1364/JOSAA.26.002327 JOAOD6 0740-3232 Google Scholar
S. RobertA. Mure-Ravaud,
“Characterization of optical diffraction gratings by use of a neural method,”
J. Opt. Soc. Am. A, 19
(1), 24
–32
(2002). http://dx.doi.org/10.1364/JOSAA.19.000024 JOAOD6 0740-3232 Google Scholar
I. Gereigeet al.,
“Recognition of diffraction-grating profile using a neural network classifier in optical scatterometry,”
J. Opt. Soc. Am. A, 25
(7), 1661
–1667
(2008). http://dx.doi.org/10.1364/JOSAA.25.001661 JOAOD6 0740-3232 Google Scholar
C. CortesV. Vapnik,
“Support-vector networks,”
Mach. Learn., 20
(3), 273
–297
(1995). http://dx.doi.org/10.1023/A:1022627411411 MALEEZ 0885-6125 Google Scholar
H. DruckerD. WuV. Vapnik,
“Support vector machine for spam categorization,”
IEEE Trans. Neural Netw., 10
(5), 1048
–1054
(1999). http://dx.doi.org/10.1109/72.788645 ITNNEP 1045-9227 Google Scholar
E. B. BaumD. Haussler,
“What size net gives valid generalization,”
Neural Comput., 1
(1), 151
–160
(1989). http://dx.doi.org/10.1162/neco.1989.1.1.151 NEUCEB 0899-7667 Google Scholar
F. KanayaS. Miyake,
“Bayes statistical behavior and valid generalization of pattern classifying neural networks,”
IEEE Trans. Neural Netw., 2
(4), 471
–475
(1991). http://dx.doi.org/10.1109/72.88169 ITNNEP 1045-9227 Google Scholar
W. Z. LuW. J. Wang,
“Potential assessment of the support vector machine method in forecasting ambient air pollutant trends,”
Chemosphere, 59
(5), 693
–701
(2005). http://dx.doi.org/10.1016/j.chemosphere.2004.10.032 CMSHAF 0045-6535 Google Scholar
X. Niuet al.,
“Specular spectroscopic scatterometry,”
IEEE Trans. Semicond. Manufact., 14
(2), 97
–111
(2001). http://dx.doi.org/10.1109/66.920722 ITSMED 0894-6507 Google Scholar
S. Aryaet al.,
“An optimal algorithm for approximate nearest neighbor searching,”
J. ACM, 45
(6), 891
–923
(1998). http://dx.doi.org/10.1145/293347.293348 JOACF6 0004-5411 Google Scholar
J. L. Bentley,
“Multidimensional binary search trees used for associative searching,”
Commun. ACM, 18
(9), 509
–517
(1975). http://dx.doi.org/10.1145/361002.361007 CACMA2 0001-0782 Google Scholar
D. T. LeeC. K. Wong,
“Worst-case analysis for region and partial region searches in multidimensional binary search trees and balanced quad trees,”
Acta. Inform., 9
(1), 23
–29
(1977). http://dx.doi.org/10.1007/BF00263763 AINFA2 0001-5903 Google Scholar
A. GionisP. IndykP. Motwani,
“Similarity search in high dimensions via hashing,”
in Proc. 25th International Conference on Very Large Data Bases,
518
–529
(1999). Google Scholar
C. W. HsuC. J. Lin,
“A comparison of methods for multiclass support vector machines,”
IEEE Trans. Neural Netw., 13
(2), 415
–425
(1999). http://dx.doi.org/10.1109/72.991427 ITNNEP 1045-9227 Google Scholar
C. C. ChangC. J. Lin,
“LIBSVM: a library for support vector machines,”
ACM Trans. Intell. Syst. Technol., 2
(3), 1
–27
(2011). http://dx.doi.org/10.1145/1961189.1961199 Google Scholar
R. M. Al-AssaadD. M. Byrne,
“Error analysis in inverse scatterometry. I. Modeling,”
J. Opt. Soc. Am. A, 24
(2), 326
–338
(2007). http://dx.doi.org/10.1364/JOSAA.24.000326 JOAOD6 0740-3232 Google Scholar
Biography Jinlong Zhu is currently a PhD candidate at Huazhong University of Science and Technology under the guidance of Shiyuan Liu. He received his BS degree from the School of Mechanical Engineering and Science of the same university in 2010. His research involves various issues in optical critical dimension (OCD) metrology, including the forward modeling with model order reduction and the inverse extraction of geometrical profiles. He is a student member of SPIE and IEEE.  Shiyuan Liu is a professor of mechanical engineering at Huazhong University of Science and Technology, leading his Nanoscale and Optical Metrology Group with research interest in metrology and instrumentation for nanomanufacturing. He also actively works in the area of optical lithography, including partially coherent imaging theory, wavefront aberration metrology, optical proximity correction, source mask optimization, and inverse lithography technology. He received his PhD in mechanical engineering from Huazhong University of Science and Technology in 1998. He is a member of SPIE, OSA, AVS, IEEE, and CSMNT (Chinese Society of Micro/Nano Technology). He holds 20 patents and has authored or co-authored more than 100 technical papers.  Chuanwei Zhang is an assistant professor at Huazhong University of Science and Technology. He received his BE and ME in mechanical engineering from Wuhan University in 2004 and 2006, respectively, and then received his PhD in mechanical engineering from Huazhong University of Science and Technology in 2009. He is currently working on optical techniques for critical dimension, overlay, and 3D profile metrology for nanomanufacturing. He is a member of SPIE, OSA, and IEEE.  Xiuguo Chen is currently a PhD candidate at Huazhong University of Science and Technology under the guidance of Shiyuan Liu. He received his MS degree from the School of Mechanical Science and Engineering of the same university in 2009. His research involves various issues in OCD metrology, including fast optical modeling and robust parameter extraction. He is a student member of OSA, ACM, and IEEE.  Zhengqiong Dong is currently a PhD candidate at Huazhong University of Science and Technology under the guidance of Shiyuan Liu. She received her BS degree in mechanical engineering from South China University of Technology in 2010. She is now focusing on the sensitivity and uncertainty analysis for OCD metrology. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||