|
|
1.IntroductionIn the last few decades, several technical breakthroughs have provided researchers with the ability to apply an external “force” to a microscopic particle in the piconewton range while measuring its position with subnanometer resolution. Since their development,1 optical tweezers (OTs) have been of great interest for their all-optical manipulation capabilities and have proven their potential in several different applications in physics as well as in biology.2 In particular, together with atomic force microscopes and magnetic tweezers,3 OTs are routinely used to study biological systems at the single-molecule level. The mechanical behavior of single biopolymers, such as DNA and the mechanochemical properties of enzymes and molecular motors can be directly probed with OT by optical forces. This is achieved by biochemically tethering the optically trapped particle, often a microbead, to the biological system under study. Using the trapped particle as a handle, force can be detected from and transferred to the molecular system. There is a growing interest in expanding the capabilities of optical manipulation by controlling and measuring the “torque” on the trapped particle.4 Several biological molecular systems are susceptible to torque and twist, parameters that are often finely controlled by living cells. Typical examples include the degree of coiling of the double-stranded DNA molecule (modified by specialized enzymes), ATP synthesis (accomplished by a rotary machine in mithochondria), and motility in many bacteria (based on a rotary motor).5 Therefore, the development of techniques that allow angular manipulation will open new methods of studying biological nanoscale systems, where rotation is a relevant physical parameter. In the angular OT implementation we employ, further termed optical torque wrench (OTW),6–8 a microscopic birefringent particle is optically trapped and angularly manipulated using the linear polarization of the laser. The particles, nanofabricated and removed from a quartz wafer, are shaped as cylinders with an aspect ratio of , a geometry that conveniently fixes the geometrical axis of the cylinder in the optical trap parallel to the laser propagation direction.9 Different protocols have been used for the fabrication of such birefringent particles. The first demonstrations of angular manipulation in OT employed irregularly shaped microcrystals,6,10 or asymmetric dielectric particles.11 Later, the advantages of the cylindrical geometry of a uniaxial-positive material were demonstrated.12 Protocols based on optical and electron beam lithography7,12,13 have been successfully used, while recently, a simpler fabrication process based on nanosphere lithography has been developed.14 However, the complexity of the fabrication techniques remains an obstacle for a more widespread use of angular manipulation in OT. Here, we propose to use a method of fabricating quartz cylinders based on laser interference lithography (LIL), a well-known, simple, fast, and inexpensive technique, which produces submicron particles suitable for optical angular manipulation and torque measurement. 2.Methods2.1.Laser Interference LithographyLIL, also known as holographic lithography, consists of the direct transfer of laser interference patterns on a photoresist, without the need of a lithography mask [Fig. 1(a)]. LIL combines the ease and speed of a direct illumination in a simple optical setup for applications, where large area () patterns of lines or dots are needed,15,16 as in our case [Fig. 1(b)]. The linear interference pattern resulting from the coincidence of two plane wavefronts has a spatial period given by where is the wavelength of the laser source and is the angle between the two beams [Fig. 1(c)]. By increasing the number of interfering light beams, it is possible to create more complex interference patterns such as arrays of dots in two or three dimensions.17 Here, we simply use two consecutive illuminations, superposing two linear interference patterns oriented at 90 deg to one another.Fig. 1Scheme of LIL. (a) Scheme of the optical setup employed to produce the interference fringes. (b) Result of the sum of two interference patterns. (c) Interference patterns generated by two light beams intersecting at an angle . (d) Schematic view of the aspect ratio of the exposed photoresist as a function of exposure. 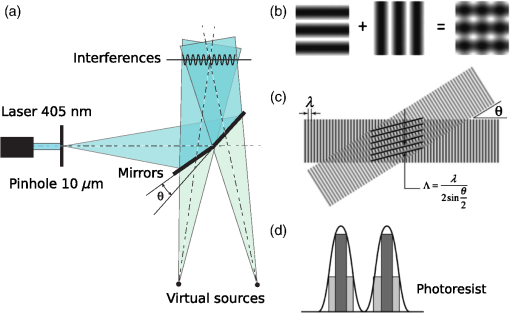 The optical setup used in our experiments is depicted in Fig. 1(a). A 30-mW laser with produces a Gaussian beam, which is focused on a wide pinhole, resulting in a coherent light beam propagating from the aperture with a coherence length larger than 10 m. The divergent beam strikes two adjacent mirrors oriented at an angle , creating two beams interfering at the plane where the sample, coated with photoresist, is placed. This interference region is about in our setup and the illuminance is , which imposes minute-long exposures for common photoresists. By adjusting the angle between the two mirrors, according to Eq. (1), we can continuously tune the spatial period of the interference and generate patterns with a pitch from 400 nm up to . The exposure duration is set to provide the required optical dose to completely cross-link the photoresist at the location of constructive interference. By controlling the exposure time, it is also possible to tune the ratio of exposed versus nonexposed photoresist and hence, to adjust the lines width or dots diameter while keeping a constant pitch [Fig. 1(d)]. 2.2.Optical Torque WrenchDepending on their spin, photons carry positive or negative angular momentum, which corresponds to the two left- and right-circular polarization components. Because of the birefringence, the polarization state of the trapping beam is modified during the propagation through the particle trapped in the laser focus. This results in a change in the total spin angular momentum of the laser beam, which reflects the torque transferred to the particle. The induced dipole moment and the laser electric field are generally not parallel in the birefringent crystal. The angle between the two vectors results in a restoring torque on the particle.6 As a consequence, the extraordinary axis of the quartz cylinder tends to orient parallel to the linear polarization of the laser. The optical torque transferred to the particle can be written as where is the angle between the laser polarization and the extraordinary axis of the cylinder and is the maximum torque (a function of laser intensity, particle geometry, and birefringence).10Our optical setup is described in detail in Refs. 8 and 18. Briefly, the trap consists of an infrared laser (, 100-mW CW at the optical trap, ) focused by a large numerical aperture objective () in a flow cell containing cylinders dispersed in water. The orientation of the linear polarization of the laser is dynamically controlled by an electro-optical modulator (EOM) combined with a quarter waveplate.7,8 In our experiments, we control the frequency of rotation of the linear polarization by driving the EOM with a sawtooth voltage signal of variable frequency. The polarization can be set in rotation in both directions with in the range from 0 to few kHz. The transferred torque is measured by analyzing the imbalance of the circular components of the polarization at the output of the trap with respect to the input. After calibration of the angular trap,18 absolute measurements of torque are performed at 20-kHz sampling rate. 3.Results3.1.Quartz Microcylinders FabricationWe depict the microfabrication process in Fig. 2. First, a chromium layer of 30 nm is sputtered onto a single-crystal quartz substrate (X-cut), previously cleaned with a Piranha solution. Second, we spin-coat a thin layer of AZ 701 MIR photoresist (Merck Performance Materials GmbH) at 4000 rpm for 30 s, followed by soft baking at 95°C for 1 min. The photoresist is diluted (2∶1) to achieve a final thickness of 600 nm. The quartz sample is then exposed on the LIL setup, prepared for a fixed interference period (typically ). Exposure is made in two steps of 130 s each, rotating the sample by 90 deg in the interference plane. After exposure, the sample is postbaked at 110°C for 1 min and developed with AZ 726 developer for 17 s under smooth agitation. Figures 3(a) and 3(b) show two SEM images of lines and dots arrays obtained after development. The next step consists in transferring the photoresist pattern onto the quartz substrate. To achieve the high anisotropy required by the cylindrical geometry, we use inductive coupled plasma reactive ion etching (ICP-RIE). To improve the selectivity of the technique (which is low especially when using photoresists), the key is to use a hard mask, as a chromium layer, and a two-step ICP-RIE process, as described below. Hard masks are often used in plasma etching, in particular to prevent photoresist shrinking,19 and the materials employed include Ni, Al, or ZnO. Abe and Esashi20 reported the etching of deep quartz trenches by using a Ni metal mask with , , and RIE gas plasma. Also, a SU8 thick photoresist has been used as a hard mask for quartz etching.21 In our case, we find that the submicron dimensions of the quartz cylinders require a thin (30 nm) hard mask layer. Following LIL patterning, the chromium layer is etched with an Ar plasma in the absence of oxygen, using a Corial 250D ICP RIE (200 W RF and 400 W LF). The absence of oxygen prevents the photoresist from shrinking during etching, allowing the unprotected hard mask to be completely removed in 6 min with sufficient selectivity. Etching of quartz is achieved by a second ICP-RIE process, using a mixture of (200 sccm) and (100 sccm), an internal pressure of 1.2 mTorr, and incoming power of 200 W RF and 800 W LF. In these conditions, the etching rate of quartz is about . Fig. 2Steps of the microfabrication process: (a) initial stack, photoresist on a 30-nm chromium layer on quartz substrate, (b) LIL and development of the photoresist, plasma sputter etching of chromium, (c) plasma etching of quartz, and (d) cleavage by microtome blade. 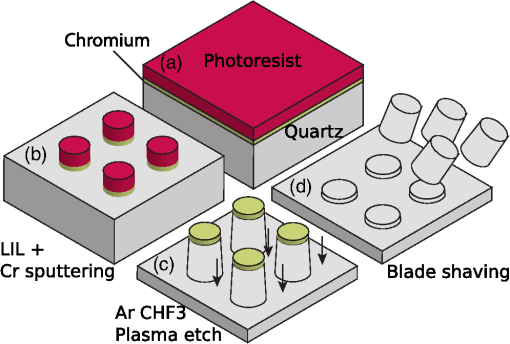 Fig. 3(a) and (b) SEM pictures of the photoresist patterns obtained by LIL: (a) lines with 800 nm pitch. (b) Dots with pitch. (c) SEM image of ICP-RIE etched quartz cylinders (45-degtilt). (d) SEM image of cylinders mechanically cleaved from the substrate.  The cylinders obtained are slightly conical, with a wall angle of about 80 deg [Fig. 3(c)]. Aiming at an aspect ratio of , we can adjust the etching time to produce cylinders with heights ranging from 900 nm to , with a homogeneity across the sample of 3% to 5%. After etching, the cylinders are mechanically cleaved and removed from the substrate by using a microtome blade, as can be observed in Fig. 3(d). They are finally collected and stored in water (a surfactant can be used to avoid coalescence). Before cleavage, the top surface of the pillars can be specifically functionalized.13 Given the dimensions of the wafer () and the pitch of the structures (), the production of cylinders would be expected. However, irregularities in the thickness of the photoresist near the edges of the substrate decrease the efficiency of the process from 60% to 70% of the total area. The distribution of sizes obtained for the cleaved cylinders, shown in Fig. 3(d), is summarized in Table 1. Table 1Cylinder size statistics for the 1-μm period series shown in Fig. 3(d) (N=35).
3.2.Optical Torque Measurement on a Trapped Birefringent CylinderIn Fig. 4, we show the dynamical measurements of the transferred torque on a single cylinder in the optical trap [sketched in Fig. 4(a)], performed for different frequencies of rotation of the linear polarization of the laser at the optical trap. As predicted by Eq. (2), when the linear polarization rotates at a frequency , the dynamical response of the system is “excitable” and can be well described by the one-dimensional motion of a particle along a tilted periodic potential.8,18 For low , the extraordinary axis of the cylinder follows the polarization rotation in phase. In this regime, the average optical torque transferred to the particle is linearly proportional to , as seen in Fig. 4(b). The time resolved torque traces are characteristic of confined Brownian motion of an angularly trapped particle, as shown in Fig. 4(c). When reaches the critical value (with given in Eq. (2) and the angular drag coefficient of the cylinder), the cylinder cannot follow in phase the rotation of the polarization. In this regime, thermal noise triggers stochastic escape events of the particle axis from the potential created by the rotating laser polarization. The average torque transferred to the particle decreases with increasing [Fig. 4(b)], and the escape events are apparent as spikes in the torque signal [Fig. 4(d)]. For larger , the rotation of the polarization is too fast to allow the particle to follow it in phase, and the average torque falls to zero [Fig. 4(b)]. The cylinder axis remains quasistatic in the trap, leading to a quasiperiodic torque trace [Fig. 4(e)]. The calibration of the optical signal allows absolute measurements of torque in physical units (pN nm) and provides a value for the angular drag coefficient of the particle immersed in water.18 Trapping one cylinder from the batch shown in Fig. 3(d), whose dimensions are distributed as indicated in Table 1, the calibration yields a value of of . This is compatible with the theoretical value of 0.9 pN nm s for a cylinder with the same dimensions.22 This dynamical behavior of the trapped cylinder, well described by the model, confirms that optical torque in the range of pN nm, relevant in single-molecule essays, can be transferred and measured on these birefringent cylinders trapped in an OTW. Fig. 4Torque measurements on a trapped cylinder. (a) Sketch of the cylinder in the optical trap: at equilibrium, the geometrical axis of the cylinder is parallel to laser propagation direction. The extraordinary axis of the crystal and the polarization of the laser are shown. (b) Average torque transferred to the particle as a function of the polarization rotation frequency . Laser power = 55 mW (blue), 92 mW (orange). (c)–(e) The instantaneous torque traces recorded at the indicated values of , as shown also in (b). 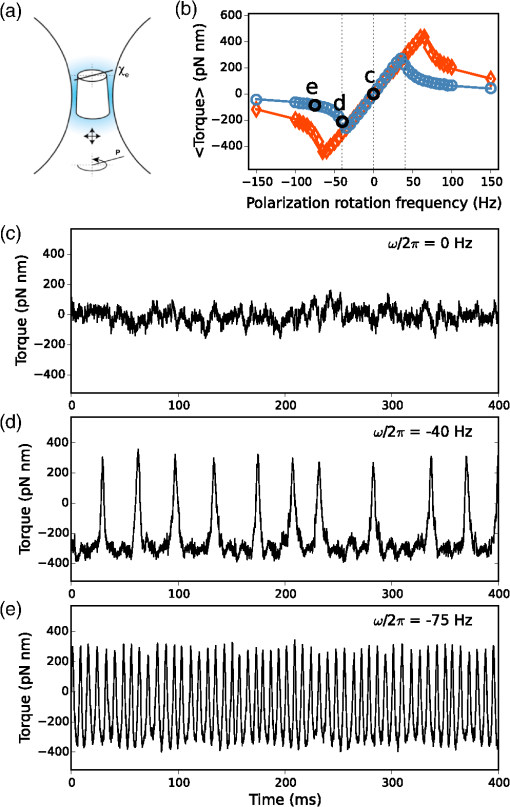 4.ConclusionsWe have presented a simple protocol based on LIL for the fabrication of quartz cylindrical particles suitable for transfer and measurement of torque in single-molecule optical manipulation essays. Based on a simple and compact optical setup, the interference-based exposure, parallel and noncontact in nature, is very well suited for the submicron cylindrical geometry required. This reduces substantially the complexity, time, and cost of the fabrication of birefringent particles used in angular measurements in optical tweezers. AcknowledgmentsWe are grateful to A. Nord for critical reading of the manuscript. We acknowledge funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 306475. ReferencesA. Ashkin, J. M. Dziedzic and T. Yamane,
“Optical trapping and manipulation of single cells using infrared laser beams,”
Nature, 330
(6150), 769
–771
(1987). http://dx.doi.org/10.1038/330769a0 Google Scholar
F. M. Fazal and S. M. Block,
“Optical tweezers study life under tension,”
Nat. Photonics, 5
(6), 318
–321
(2011). http://dx.doi.org/10.1038/nphoton.2011.100 NPAHBY 1749-4885 Google Scholar
K. C. Neuman and A. Nagy,
“Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy,”
Nat. Methods, 5 491
–505
(2008). http://dx.doi.org/10.1038/nmeth.1218 1548-7091 Google Scholar
M. Padgett and R. Bowman,
“Tweezers with a twist,”
Nat. Photonics, 5
(6), 343
–348
(2011). http://dx.doi.org/10.1038/nphoton.2011.81 NPAHBY 1749-4885 Google Scholar
J. Lipfert et al.,
“Torque spectroscopy for the study of rotary motion in biological systems,”
Chem. Rev., 115
(3), 1449
–1474
(2015). http://dx.doi.org/10.1021/cr500119k Google Scholar
A. La Porta and M. D. Wang,
“Optical torque wrench: angular trapping, rotation, and torque detection of quartz microparticles,”
Phys. Rev. Lett., 92
(19), 190801
(2004). http://dx.doi.org/10.1103/PhysRevLett.92.190801 PRLTAO 0031-9007 Google Scholar
B. Gutierrez-Medina et al.,
“An optical apparatus for rotation and trapping,”
Methods Enzymol., 475 377
–404
(2010). http://dx.doi.org/10.1016/S0076-6879(10)75015-1 MENZAU 0076-6879 Google Scholar
F. Pedaci et al.,
“Excitable particles in an optical torque wrench,”
Nat. Phys., 7
(3), 259
–264
(2010). http://dx.doi.org/10.1038/nphys1862 NPAHAX 1745-2473 Google Scholar
Y. Cao et al.,
“Equilibrium orientations and positions of non-spherical particles in optical traps,”
Opt. Express, 20
(12), 12987
–12996
(2012). http://dx.doi.org/10.1364/OE.20.012987 OPEXFF 1094-4087 Google Scholar
M. E. J. Friese et al.,
“Optical alignement and spinning of laser-trapped microscopic particles,”
Nature, 394 348
–350
(1998). http://dx.doi.org/10.1038/28566 Google Scholar
L. Oroszi et al.,
“Direct measurement of torque in an optical trap and its application to double-strand DNA,”
Phys. Rev. Lett., 97 058301
(2006). http://dx.doi.org/10.1103/PhysRevLett.97.058301 Google Scholar
C. Deufel et al.,
“Nanofabricated quartz cylinders for angular trapping: DNA supercoiling torque detection,”
Nat. Methods, 4 223
–225
(2007). http://dx.doi.org/10.1038/nmeth1013 1548-7091 Google Scholar
Z. Huang et al.,
“Electron beam fabrication of birefringent microcylinders,”
ACS Nano, 5
(2), 1418
–1427
(2011). http://dx.doi.org/10.1021/nn1034108 ANCAC3 1936-0851 Google Scholar
P.-C. Li et al.,
“Fabrication of birefringent nanocylinders for single-molecule force and torque measurement,”
Nanotechnology, 25
(23), 235304
(2014). http://dx.doi.org/10.1088/0957-4484/25/23/235304 NNOTER 0957-4484 Google Scholar
Q Xie et al.,
“Fabrication of nanostructures with laser interference lithography,”
J. Alloys Compd., 449
(1), 261
–264
(2008). http://dx.doi.org/10.1016/j.jallcom.2006.02.115 JALCEU 0925-8388 Google Scholar
J. De Boor et al.,
“Sub-100 nm silicon nanowires by laser interference lithography and metal-assisted etching,”
Nanotechnology, 21
(9), 095302
(2010). http://dx.doi.org/10.1088/0957-4484/21/9/095302 NNOTER 0957-4484 Google Scholar
M. Maldovan and E. L. Thomas, Periodic Materials and Interference Lithography: For Photonics, Phononics and Mechanics, John Wiley & Sons, Weinheim, Germany
(2009). Google Scholar
F. Pedaci et al.,
“Calibration of the optical torque wrench,”
Opt. Express, 20 3787
–3802
(2012). http://dx.doi.org/10.1364/OE.20.003787 OPEXFF 1094-4087 Google Scholar
L. Li, T. Abe and M. Esashi,
“Fabrication of miniaturized bi-convex quartz crystal microbalance using reactive ion etching and melting photoresist,”
Sens. Actuators, A, 114
(2), 496
–500
(2004). http://dx.doi.org/10.1016/j.sna.2003.12.031 Google Scholar
T. Abe and M. Esashi,
“One-chip multichannel quartz crystal microbalance (QCM) fabricated by deep RIE,”
Sens. Actuators A, 82
(1), 139
–143
(2000). http://dx.doi.org/10.1016/S0924-4247(99)00330-1 Google Scholar
H. Chen and C. Fu,
“An investigation into the characteristics of deep reactive ion etching of quartz using su-8 as a mask,”
J. Micromech. Microeng., 18
(10), 105001
(2008). http://dx.doi.org/10.1088/0960-1317/18/10/105001 JMMIEZ 0960-1317 Google Scholar
M. M. Tirado and J. G. de La Torre,
“Rotational dynamics of rigid, symmetric top macromolecules. Application to circular cylinders,”
J. Chem. Phys., 73 1986
(1980). http://dx.doi.org/10.1063/1.440288 Google Scholar
|

